cryptopals
Solutions to all cryptopals problems: Sets 1-7, Set 8.
The only dependency on top of standard JRE 17 runtime is that on Lombok. The project runs on all subsequent versions of the Java platform such as Java 21 and Java 23.
Additional dependencies:
- Spring Boot 3.x for problems requiring a server side part in addition to a client part
- The GNU Multiple Precision Arithmentic Library (GMP) and the JNA-GMP wrapper for it for a more optimized implementation of modular exponentiation than that provided by BigInteger::modPow. This is relevant only for a few challenges starting with Challenge 48.
- GraalJS engine for Challange 50. In the past JRE provided a JavaScript engine called Nashorn, but this was discontinued in Java15.
How to run
The majority of the challenges of a set can be run by executing the com.cryptopals.Setx.main method of the set or
by running the JUnit5 tests found under src/test/java/com/cryptopals/SetXTests.
Required dependencies are defined in the project’s pom.xml.
Some challenges (31,
32, 34,
35, 36,
37, 49,
57, 58,
59, 60,
66) require a server-side application.
This can be produced with mvn install and executed with
java -jar cryptopals_server-0.2.0.jar
as a typical SpringBoot 3.x application. This application provides either a RESTful API or an RMI component depending on a challenge.
For the more advanced problems I created a proper explanation about the implementation of each of these attacks, which you can find in the Table of Contents below.
Table of Contents
- Set 6: RSA and DSA
- Set 7: Hashes
- Set 8: Abstract Algebra
- Challenge 57. Diffie-Hellman Revisited: Small Subgroup Confinement
- Challenge 58. Pollard’s Method for Catching Kangaroos
- Challenge 59. Elliptic Curve Diffie-Hellman and Invalid-Curve Attacks
- Challenge 60. Single-Coordinate Ladders and Insecure Twists
- Challenge 61. Duplicate-Signature Key Selection in ECDSA (and RSA)
- Challenge 62. Key-Recovery Attacks on ECDSA with Biased Nonces
- Challenge 63. Key-Recovery Attacks on GCM with Repeated Nonces
- Challenge 64. Key-Recovery Attacks on GCM with a Truncated MAC
- Challenge 65. Truncated-MAC GCM Revisited: Improving the Key-Recovery Attack via Ciphertext Length Extension
- Challenge 66. Exploiting Implementation Errors in Diffie-Hellman
- Additional problems
Set 6: RSA and DSA
Challenge 48. Bleichenbacher’s PKCS 1.5 Padding Oracle (Complete Case)
Challenge 48 is fairly straightforward to implement by following the steps in Section 3.1 Description of the Attack of Bleichenbacher’s Chosen Ciphertext Attacks Against Protocols Based on the RSA Encryption Standard PKCS #1 paper. An important observation is that thanks to Step 2c the attack runs in O(log(n)), where n is the size of the RSA modulus.
I created a helper class to aid this process. When following the paper, one needs to pay particular attention to rounding in all the equalities. For example I ended up waisting a lot of time with Inequality (2) in Step 2c:
2B + ri·n 3B + ri·n
--------- <= si < --------- (2)
b a
Initially I implemented it by letting si iterate from the lower bound until (not including) the upper bound. However
that resulted in an incorrect implementation. The term on the right of Inequality (2) will most likely not be an integer
value. Therefore, when computed using infinite precision integers, it will be less than its counterpart computed over reals.
As a result the correct way to implement Step 2c is to let si go to (including) the upper bound when the upper bound
is rounded down to an integer:
while (true) {
BigInteger lower = divideAndRoundUp(_2B.add(rn), interval.upper),
upper = _3B.add(rn).divide(interval.lower);
for (BigInteger nextS=lower; nextS.compareTo(upper) <= 0; nextS = nextS.add(ONE)) {
if (paddingOracle.test(pubKey.encrypt(nextS).multiply(cipherText))) return s = nextS;
}
rn = rn.add(pubKey.getModulus());
}
Practical optimization to tackle real world length RSA moduli
The challenge suggests to go all the way up to 768-bits moduli. With my first implementation using Java’s BigInteger it takes about 30 seconds. Yet, in the real world such small RSA moduli are long a relic of the past. Trying to go for 1024-bits moduli and longer let the implementation spin for longer than I wanted to wait. To address that I switched to an optimized implementation of infinite precision integers based on The GNU Multiple Precision Arithmentic Library (GMP). Thanks to the JNA-GMP wrapper this was very easy to do. If you are on macOS, you probably already installed gmp when you installed Python with Homebrew.
With tiny changes to the RSAHelper and RSAHelperExt classes the speedup was remarkable. With GMP 6.2.0 I was able to go all the way to 2048-bits moduli within just a couple of minutes:
| RSA modulus size | Average duration of attack (20 tries) |
|---|---|
| 256 bits | 2 s 262 ms |
| 768 bits | 7 s 207 ms |
| 1024 bits | 19 s 271 ms |
| 1536 bits | 39 s 213 ms |
| 2048 bits | 1 m 54s 607 ms |
This difference between the performance of JRE’s implementation of BigIntegers and that of GMP is quite remarkable and goes somewhat against Joshua Bloch’s advice given in “Item 66: Use native methods judiciously” of his excellent “Effective Java, 3rd edition” book. His reply to my tweet confirmed that.
/**
* @param numBits number of bits in each prime factor of an RSA modulus, i.e. the modulus is thus {@code 2*numBits} long
*/
@DisplayName("https://cryptopals.com/sets/6/challenges/47 and https://cryptopals.com/sets/6/challenges/48")
@ParameterizedTest @ValueSource(ints = { 128, 384, 512, 768, 1024 })
void challenges47and48(int numBits) {
RSAHelperExt rsa = new RSAHelperExt(BigInteger.valueOf(17), numBits);
BigInteger plainText = RSAHelperExt.pkcs15Pad(CHALLANGE_47_PLAINTEXT.getBytes(),
rsa.getPublicKey().getModulus().bitLength());
BigInteger cipherTxt = rsa.encrypt(plainText);
BigInteger crackedPlainText = PaddingOracleHelper.solve(cipherTxt, rsa.getPublicKey(), rsa::paddingOracle);
assertArrayEquals(CHALLANGE_47_PLAINTEXT.getBytes(), rsa.pkcs15Unpad(crackedPlainText));
}
Conclusions
Bleichenbacher’s attack clearly demonstrates that RSA-PKCS1 v1.5 encryption is not CCA-secure. A truly CCA-secure public key encryption system cannot be broken even given a full decryption oracle (this is by definition of CCA security for public key encryption), while Bleichenbacher’s attack merely uses a partial oracle. Is the fix that was implemented in TLS 1.0 sufficient to make RSA-PKCS1 v1.5 CCA secure? Likely, but there’s no security proof. This is the main reason v2.0 of RSA-PKCS1 adopted Optimal Asymmetric Encryption Padding (OAEP) for RSA encryption, for which there’s a security proof that the resulting scheme is CCA secure under certain assumptions.
Set 7: Hashes
Challenge 49. CBC-MAC Message Forgery
The second part of this challenge, which deals with a message length extension attack for a multiple transactions request:
Your mission: capture a valid message from your target user. Use length extension to add a transaction paying the attacker’s account 1M spacebucks.
assumes that the attacker and the victim share the same authentication key, which is quite a stretch.
Challenge 52. Iterated Hash Function Multicollisions
Challenge 52 is one of the best demonstrations of the birthday paradox I’ve seen. NB: the way this challenge defines the compression function containts a mistake. The correct definition should be
function MD(M, H, C):
for M[i] in pad(M):
H := C(M[i], H) ^ H
return H
For the purposes of this task it makes sense to choose a cipher whose key size is 8 bytes. It will also be easier
if the cipher’s key and block sizes are the same. I opted for Blowfish, which is present in all JREs through
com.sun.crypto.provider.SunJCE provider. I used a 16 bit hash for the easier hash function f, and a 32 bit hash for g.
This way I needed to find 216 messages colliding in f to ensure there’s a pair among them colliding in g.
Challenge 54. Kelsey and Kohno’s Nostradamus Attack
Challenge 54 shows an ingenious way of finding a target collision between a Merkle–Damgård
hash of two messages m0 and m1, where m0 is chosen arbitrarily by the attacker while
m1 is not and needs to be augmented with a suffix that would make its hash match that of m0.
The only requirement is that |m0| > |m1| by a few blocks. The number of blocks
by which the length of m0 exceeds the length of m1 is referred to as k. The way this challenge
is presented is in the form of using hashes to produce commitments.
The attack is explained at length by John Kelsey and Tadayoshi Kohno in
their Herding Hash Functions and the Nostradamus Attack paper. The most
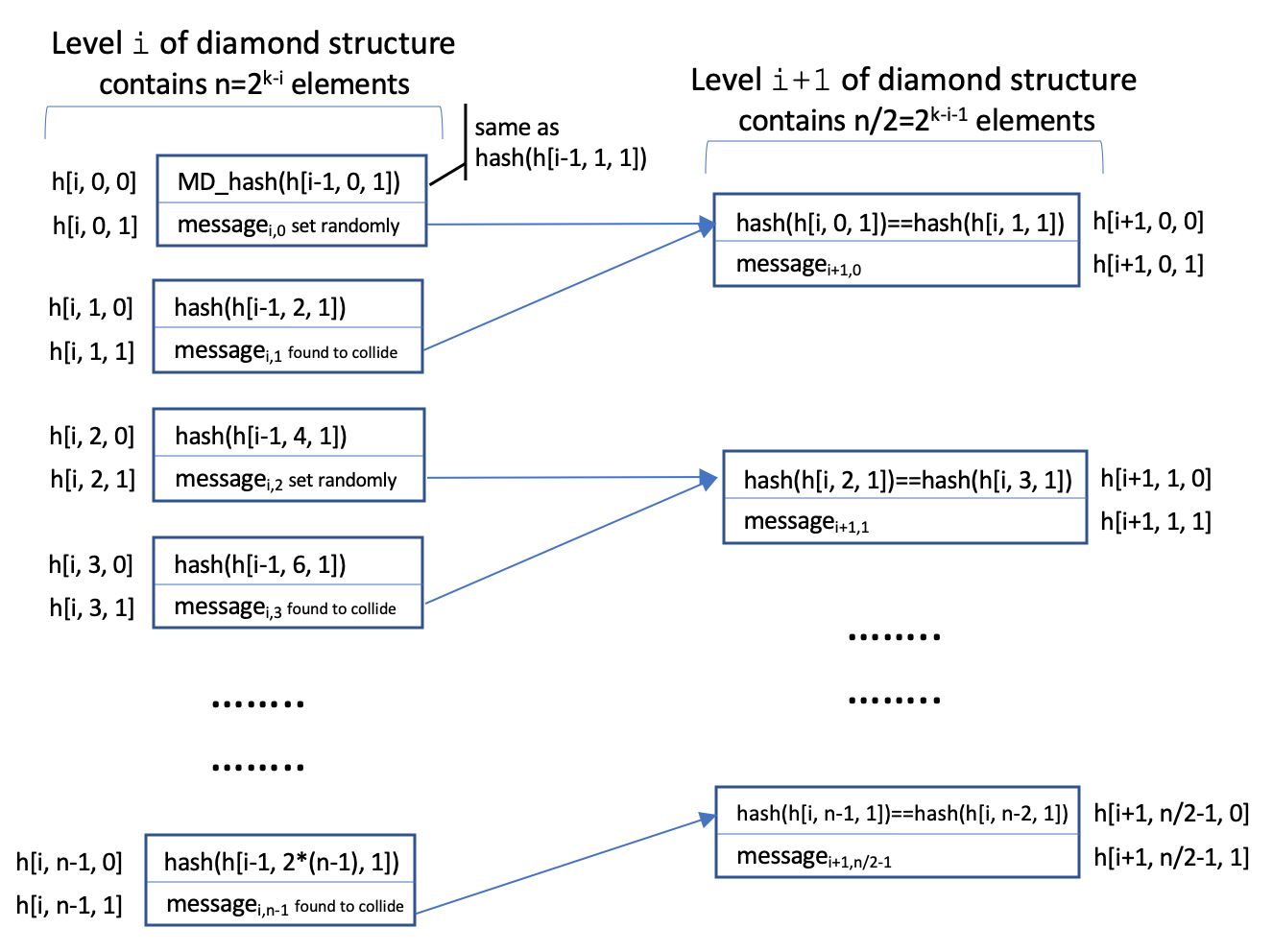
involved part of the attack is building the diamond structure. I decided to represent it as a multi dimensional array.
The first dimension (i) is the tree level, the second (j) contains 2k-i two-element arrays in which the first element
is the starting hash h[i, j] (i.e. the chaining variable) and the second element is a message block whose hash collides
with that of the message starting at either h[i, j+1] (when j is even) or h[i, j-1] (when j is odd). I demonstrate this
in the following picture:
 To make working with the diamond structure easier I created the DiamondStrcuture class,
which encapsulates it.
To make working with the diamond structure easier I created the DiamondStrcuture class,
which encapsulates it.
Level 0 of the array is special in that all the hashes stored in h[0, j, 0] are the initial chaining variables
and can be set at will. I decided to populate the elements h[0, j, 0] in such as way as to ensure that they are sorted.
This allows me to make use of a binary search when I need to construct a k-blocks long suffix for m1. The
construction of level i of the diamond structure calls for finding 2k-i message blocks whose hash matches
a given target. I created MDHelper::findCollisionsWith
helper method to make it easier. To speed up the construction of a given level, I observed that this task
lends itself to parallelization.
This sped up the process a lot.
Some other notes worth mentioning. I use m0 of 14 blocks long and m1 of 4 blocks. This gives me
a diamond structure with 10 levels and 210 different initial hashes at level 0. I make use of the easy 16-bit hash f
from Challenge 52. With this setup I am able to construct the desired Nostradamus message in about 11 minutes on
my MacBook Pro (with 8 virtual cores).
@Test
void challenge54() throws NoSuchAlgorithmException, NoSuchPaddingException, BadPaddingException, InvalidKeyException, IllegalBlockSizeException, ExecutionException, InterruptedException {
byte[] H = {0, 1}, H2 = {0, 1, 2};
MDHelper mdHelper = new MDHelper(H, H2, "Blowfish", 8);
String originalCommittedToMsg = /* 14 blocks, 2^10 */
"3-5, 0-0, 1-6, 4-2, 2-2, 4-3, 1-1 dummy prediction that will be replaced"
+ "1234567887654321012345677654321012345678",
nostradamusMsg = "3-1, 0-1, 2-6, 2-2, 3-1, 1-1,0-3"; /* 4 blocks */
byte[] hash = mdHelper.mdEasy(originalCommittedToMsg.getBytes()),
trgtHash = mdHelper.mdInnerLast(originalCommittedToMsg.getBytes(), H,
0, originalCommittedToMsg.length() / 8), sfx;
DiamondStructure ds = new DiamondStructure(
originalCommittedToMsg.length() - nostradamusMsg.length() >> 3,
trgtHash, "Blowfish", 8);
sfx = ds.constructSuffix(mdHelper.mdInnerLast(nostradamusMsg.getBytes(), H, 0, 4));
if (sfx != null) {
assertEquals(originalCommittedToMsg.length(), nostradamusMsg.length() + sfx.length);
byte longMsg[] = Arrays.copyOf(nostradamusMsg.getBytes(), nostradamusMsg.length() + sfx.length);
System.arraycopy(sfx, 0, longMsg, nostradamusMsg.length(), sfx.length);
assertArrayEquals(hash, mdHelper.mdEasy(longMsg));
} else {
fail("Too few leaves in the diamond structure :-(");
}
}
Conclusions
It is not safe to produce a commitment just by hashing a secret message m with a collision-resistant hash function. There’s no
security proof that such a construction is safe. The correct way to produce a commitment for a secret message m
is to generate a uniformly distributed random number r of, say 512 bits if SHA256 is used as a collision-resistant hash function.
Then compute h = SHA256(r || m). The commitment is a pair (r, h), of which h is revealed while r is kept secret until
it comes time to prove knowledge of m. However the attack presented in this challenge will still work with this correct setup
since the person making the prediction is in control of r.
This attack shows that producing a commitment by hashing a secret message m with a hash function that is built using
the Merkle–Damgård construction may not guarantee the binding property of the commitment, which a cryptographically secure
commitment scheme must possess (in addition to that of hiding m). If a hash function is target collision resistant,
using it to produce commitments would be safe.
Why does this attack work? The main reason is that hash functions employing the Merkle–Damgård construction are vulnerable to message-length extension attacks. That’s the main reason the recently standardized by NIST SHA3 hash standard uses the sponge construction instead of Merkle–Damgård. Using SHA3 for making commitments is immune from this attack. So would be using HMAC0 with SHA256 as the underlying hash: HMAC0(m) := HMAC(0l, m) = H(opad || H(ipad || m))
How feasible would mounting this attack be against SHA256? In their original paper the authors indicate that it reduces
the effort required for finding a collision with the target hash from O(2256) to O(2172) when
k=84, i.e. |m0| is greater than |m1| by 84 512-bit blocks (or by 5.25 KiB). The space complexity
of such a diamond structure would be huge. Level 0 alone would take up 284 * (64 + 32) bytes, which is
1536 YiB yobibyte (1 yobibyte == 280 bytes) — a mind-boggling number. This makes this attack infeasible
against SHA-256 in my opinion. Using shorter hashes from the MD family for making commitments is indeed risky.
Challenge 55. MD4 Collisions
Challenge 55 is probably one of the most interesting to work on in the first 7 sets. I succeeded in implementing it in a uniform Object-Oriented way, which aids readability and maintainability. The implementation is also blazingly fast — it finds a collison within a few seconds. Here is one found with it:
Collision found between
683E10B651E9185B4D9886D90B7634AE7C4D753533F75041C388E6ACF20CF8B12BA9C27368F09B22EDCE3445BBFED7E8636EDB70070DF0EB7449FA54E421D246
683E10B651E918DB4D9886490B7634AE7C4D753533F75041C388E6ACF20CF8B12BA9C27368F09B22EDCE3445BBFED7E8636EDA70070DF0EB7449FA54E421D246
MD4: B9B0031B30D53E826B80CBDDBE7354D9
I succeeded in fully enforcing all constraints from the first round of MD4 as well as all constraints from the first two steps of the second round. I didn’t figure out how to apply the constraints from the 3rd step of the second round of MD4. X. Wang et al. give some hints in their paper, yet they are not easy to follow
Utilize more precise modification to correct some other conditions. For example, we can use the internal collision in Table 2 in which there are three message words are changed to correct c5,i, i = 26, 27, 29, 32. The precise modification should add some extra conditions in the first rounds (see Table 2) in advance. There are many other precise modifications. c5,30 can be corrected by other modification. By various modifications, besides two conditions in the third round, almost all the conditions in rounds 1-2 will be corrected. The probability can be among 2^6 ∼ 2^2.
It is interesting to note that X. Wang et al. used differential cryptanalysis to discover the conditions that lead to collisions in MD4. MD4 was developed in 1990 by Ron Rivest, which is also the year in which Eli Biham and Adi Shamir introduced differential cryptanalysis. Obviously the designer of MD4 didn’t take it into account while designing MD4. Interestingly, the NSA discovered differential cryptanalysis as early as in the 1970s, which is one of the reasons why DES is immune to it (see this paper or Section 12.4 in Bruce Schneier’s Applied Cryptography 2nd edition for details).
Challenge 56. RC4 Single-Byte Biases
Challenge 56 is an excellent demonstration of how even a tiny bias that makes the distribution of a secure PRF slightly different from uniform might be enough to break it. In the case of RC4 bytes 2 to 255 of RC4 keystream have biases on the order of 1/216 or higher.
This challenge is based on the attack outlined in Section 4.1 of this paper. In my solution I used the biases in the 16th (Z16) and 32nd (Z32) bytes of RC4’s keystream, which are elucidated in Section 3.1 of the paper.
The essence of this attack is fairly simple — the biases in the distributions of Z16 and Z32 make
the frequency of a few values much higher than 1/256 (0x00, 0xF0, 0x10 for Z16;
and 0x00, 0xE0, 0x20 for Z32). If we ensure that we encrypt the same plaintext bytes in these positions
repeatedly, certain ciphertext values for C16 and C32 will also occur more frequently than others.
By encrypting on the order of 224 values, we construct the distribution of C16 and C32,
which (like the distribution of Z16 and Z32) will not be uniform. This is enough to recover the
original plaintext bytes P16 and P32 using the maximum-likelihood estimation.
Since the biases in Z16 and Z32, while non-negligible, are still fairly small, I used 227 RC4 keystreams (with independent 128-bit keys) to construct their frequency distributions. With smaller values such as 225 or less, the recovered plaintext cookie will contain errors, particularly for P32. BTW: In the paper Nadhem J. AlFardan et al. used 244 RC4 keystreams to determine the disributions of Z16 and Z32. For this challenge this would be an overkill.
For the maximum-likelihood estimation of the plaintext bytes I used 224 ciphertexts. This is enough to recover P16 and P32 and fully corraborates the results in Figure 4 in the paper.
Set 8: Abstract Algebra
This set of problems is amazingly interesting, however it took me approximately twice as long as the previous sets combined. It also calls for creating some handy software that might be of use beyond solving these challenges: such as code for elliptic curve cryptography, various ways for calculating dlog, code for GCM along with its GHASH one-time-hash, code for finding roots of polynomials over different fields, matrix operations over GF(2), matrix operations over R, etc.
Challenge 57. Diffie-Hellman Revisited: Small Subgroup Confinement
Challenge 57 introduces the Pohlig-Hellman
algorithm. The best general-purpose algorithm for taking discrete logs in Zp* is
the General Number Field Sieve (GNFS). The running time
of the GNFS is O(∛p), where p is the group’s prime.
The Pohlig-Hellman algorithm lets take discrete logs potentially faster than that for groups where n = p-1 (the order of Zp*)
has many small factors. Moreover it works for any cyclic group — the fact that will come in handy in Challenge 59.
If n = p1e1 · p2e2 · … · prer, then
the computational complexity of taking dlog with Pohlig-Hellman is O{Σ[ei · (lgn + √pi)]}.
Well, the way @spdevlin proposes to go about the solution, which is the path I took:
Friendly tip: maybe avoid any repeated factors. They only complicate things.
the complexity will be O[Σ(lgn + √pi)], where n <= p1 · p2 · … · pr.
Probably the most involved part of Pohlig-Hellman is a need to implement Garner’s algorithm to reconstruct Bob’s private key from its residues per subset of the moduli of p-1.
All in all the challenge presents an attack that can bypass DH implementations where Bob makes some rudimentary checks on the offered subgroup description (p, q, g):
- Are both p and q prime?
- Does q divide p-1?
- Is g different from 1?
- Is gq equal 1?
The challenge does make two big assumptions though, namely that
- Bob will naively hang on to the same private key across all new sessions with Alice.
- That group Zp* contains a large number of subgroups with small order. The attack will for example not work if p is a safe prime.
Challenge 58. Pollard’s Method for Catching Kangaroos
Challenge 58 makes the attack from the previous challenge yet more realistic.
It can be mounted against a group where p-1 has at least one large factor in addition to q (the order of a generator used).
The attack makes use of J.M. Pollard’s Lambda Method for Catching Kangaroos, as outlined in
Section 3 of Pollard’s paper.
While not as efficient as the GNFS, Pollard’s kangaroo algorithm can be applied to any cyclic group (e.g. not only to Zp*
but also to elliptic curve groups) — a fact that will be of use in a later elliptic curve challenge.
Its running time is O(√q), where q is the order of the generator used.
Pollard’s method employs a pseudo-random mapping function f that maps from set {1, 2, …, p-1} to set {0, 1, … k-1}. The challenge suggested the following simplistic definition for f (which is similar to what Pollard gives in one of his examples):
f(y) = 2^(y mod k)
I used ceil(log2√b + log2log2√b - 2) for calculating k, which is based on
the suggestion in Section 3.1 of this paper by Ravi Montenegro and Prasad Tetali.
When deciding on the amount of jumps N that the tame kangaroo is to make, I used the suggestion from the challenge description and set N to the mean of range of f multiplied by 4. With this choice of the constant the probability of Pollard’s method finding the dlog is 98%.
I generate group Zp* as follows:
pis a 1024-bit prime meeting the following requirement:p = Nq + 1, whereqis a 42-bit prime. This is based on the advice from Section 11.6 of “Cryptography Engineering, 2nd edition” by Niels Ferguson, Bruce Schneier, and Tadayoshi Kohno.- The generator
gis a random member of Zp* that has an order ofq.
The only deviation from the book is that I use fewer than 256 bits for q, which obviously weakens the group. Unfortunately
Pollard’s kangaroo algorithm doesn’t lend itself to parallelisation so choosing q to be much larger than 42 bits makes the
attack impractical. E.g. with a 42-bit q the attack takes on the order of 20 minutes on my MacBook Pro.
To make the attack more realistic I establish only one session to Bob to find b mod r, where r is one factor of N.
This no longer assumes that Bob uses the same private key across all new sessions with Alice. The attack thus works
in a realistic setting where Bob generates a new private key for each new session.
NB: The attack will still be infeasible if p is chosen to be a safe prime. However such choices of Zp*
are rare as they lead to more computationally intensive exponentiation in the group.
Challenge 59. Elliptic Curve Diffie-Hellman and Invalid-Curve Attacks
Challenge 59 is based on the Weierstrass form of representing elliptic curves: y2 = x3 + ax + b
When implementing the group operation in E(Fp), division should be carried out as multiplication by the multiplicative inverse mod p, e.g.:
function combine(P1, P2):
if P1 = O:
return P2
if P2 = O:
return P1
if P1 = invert(P2):
return O
x1, y1 := P1
x2, y2 := P2
if P1 = P2:
m := ( (3*x1^2 + a) * modInv(2*y1, p) ) mod p
else:
m := ( (y2 - y1) * modInv(x2 - x1, p) ) mod p
x3 := ( m^2 - x1 - x2 ) mod p
y3 := ( m*(x1 - x3) - y1 ) mod p
return (x3, y3)
For convenience’s sake I implemented the class that represents elements of the curve so that each coordinate
of a point (x, y) is positive, i.e. x and y are stored mod p. This makes the implementation simpler.
For the rest the attack is pretty similar to Challenge 57 except that the group given in the challenge
ECGroup(modulus=233970423115425145524320034830162017933, a=-95051, b=11279326, order=233970423115425145498902418297807005944)
doesn’t have an order with many small factors. Therefore instead of finding generators of the small subgroups of this elliptic curve group, the attack hinges on Alice foisting on Bob bogus public keys that are not on the original elliptic curve but are rather on specially crafted curves
ECGroup(modulus=233970423115425145524320034830162017933, a=-95051, b=210, order=233970423115425145550826547352470124412)
ECGroup(modulus=233970423115425145524320034830162017933, a=-95051, b=504, order=233970423115425145544350131142039591210)
ECGroup(modulus=233970423115425145524320034830162017933, a=-95051, b=727, order=233970423115425145545378039958152057148)
The orders of these elliptic curves do have many small factors. Interestingly all the three crafted curves are required
to recover Bob’s private key. This is because the product of the small factors of each of these curves is less than
the order of the generator given for the challenge (182, 85518893674295321206118380980485522083). You need the distinct
small factors collected from all the crafted curves.
NB the algorithm suggested in Challenge 57 and this one for finding subgroups of required order
Suppose the group has order q. Pick some random point and multiply by q/r. If you land on the identity, start over.
only works for cyclic groups. For Challenge 57 it didn’t matter much because Zp* is always
cyclic. This doesn’t always hold for elliptic curve groups though, i.e. not every elliptic curve group is cyclic. In fact you
will not be able to find a generator of order 2 for y^2 = x^3 - 95051*x + 210 if you use the order of the group
- The correct way to find generators of required order is to use the order of the largest cyclic subgroup of an elliptic curve. For this curve it is 116985211557712572775413273676235062206. See my discussion with @spdevlin. Worth noting here that any group of a prime order is cyclic. That’s one of the reasons why some popular elliptic curves such as secp256r1 or secp256k1 have prime orders. The converse is not always true, i.e. there can be groups of non-prime order that are cyclic.
The attack in this challenge does make two assumptions though, namely that
- Bob will hang on to the same private key across all new sessions with Alice. This is the same as in Challenge 57.
- Bob will not check whether Alice’s public key lies on the expected elliptic curve. How big of an assumption
is that? Unfortunately not too big because in many implementations of ECDH Bob is only sent the x coordinate of
Alice’s public key for the sake of efficiency, and the implementation doesn’t check if x3 + ax + b is
a quadratic residue. In fact such an attack can be pulled off on the ubiquitous NIST P256 curve. It takes
a twist-secure elliptic curve such as 25519 to foil this attack. Or one can just check if Alice’s public key
is on the expected curve, e.g. the following check by Bob will render this attack harmless:
public Set8.Challenge59ECDHBobResponse initiate(ECGroup.ECGroupElement g, BigInteger q, ECGroup.ECGroupElement A) throws RemoteException { // A bit contrived for Bob to hang on to the same private key across new sessions, however this is what // Challenge 59 calls for. if (ecg == null || !ecg.equals(g.group()) || !this.g.equals(g)) { ecg = g.group(); this.g = g; privateKey = new DiffieHellmanHelper(ecg.getModulus(), q).generateExp().mod(q); } // Is Alice's public key on the curve? if (!ecg.containsPoint(A)) { throw new RemoteException("Public key presented not on the expected curve"); }
Challenge 60. Single-Coordinate Ladders and Insecure Twists
Challenge 60 is based on the Montgomery form of representing elliptic curves: Bv2 = u3 + Au2 + u
A Montgomery form curve equation can always be changed into the Weierstrass form, the converse is not always true.
Given isomorphism between EC groups of the same order regardless of their form, I abstracted the concept of
an EC point into an interface and refactored the rest of the classes accordingly. This ensured a shared implementation
of the scale and dlog methods:
public interface ECGroupElement {
BigInteger getX();
BigInteger getY();
ECGroupElement getIdentity();
ECGroupElement inverse();
ECGroupElement combine(ECGroupElement that);
ECGroup group();
/** Returns the x coordinate of kP where P is this point */
BigInteger ladder(BigInteger k);
default ECGroupElement scale(BigInteger k) {
ECGroupElement res = getIdentity(), x = this;
while (k.compareTo(BigInteger.ZERO) > 0) {
if (Set5.isOdd(k)) res = res.combine(x);
x = x.combine(x);
k = k.shiftRight(1);
}
return res;
}
}
Analogously for the concept of an EC group:
public interface ECGroup {
/** Returns the order of field F<sub>p</sub> */
BigInteger getModulus();
/** Returns the order of this curve, i.e. the number of points on it. */
BigInteger getOrder();
/** If this group is cyclic, returns its order. Otherwise returns the order of the largest cyclic subgroup. */
BigInteger getCyclicOrder();
/** Returns the identity element of this group */
ECGroupElement getIdentity();
/**
* Returns the order of the quadratic twist of this curve
*/
default BigInteger getTwistOrder() {
return getModulus().multiply(TWO).add(TWO).subtract(getOrder());
}
/**
* Calculates the y coordinate of a point on this curve using its x coordinate
*/
BigInteger mapToY(BigInteger x);
/** Checks if the point {@code elem} is on this curve */
boolean containsPoint(ECGroupElement elem);
/** Creates a point on this curve with designated coordinates */
ECGroupElement createPoint(BigInteger x, BigInteger y);
BigInteger ladder(BigInteger x, BigInteger k);
}
NB For a Montgomery curve the point at infinity O is always (0, 1). Each Montgomery curve has at least one point of order 2, it is always (0, 0).
This challenge turned out to be one of the toughest so far. Here Alice sends Bob only the x-coordinate of her public key.
Bob then derives the DH symmetric key using the Montgomery ladder: group.ladder(xA, b), where xA is the
x-coordinate of Alice’s public key and b is Bob’s private key. Bob also sends back to Alice only the x-coordinate of
his public key: g.ladder(privateKey), where g is the generator of the EC group.
What makes this challenge much more computationally intensive is that when the protocol uses only the x-coordinates of Alice’s public key, Alice never learns the exact residues of Bob’s private key when she foists public keys that are in fact generators of small subgroups. @spdevlin, the author of the challenge, gives a small hint:
HINT: You may come to notice that ku = -ku, resulting in a combinatorial explosion of potential CRT outputs. Try sending extra queries to narrow the range of possibilities.
By way of illustration. In this challenge we work with a Montgomery curve
MontgomeryECGroup(modulus=233970423115425145524320034830162017933, A=534, B=1, order=233970423115425145498902418297807005944, cyclicOrder=233970423115425145498902418297807005944)
which is isomorphic to
WeierstrassECGroup(modulus=233970423115425145524320034830162017933, a=-95051, b=11279326, order=233970423115425145498902418297807005944, cyclicOrder=233970423115425145498902418297807005944)
from the previous challenge.
The twist of our Montgomery curve has order 2·modulus + 2 - order-of-curve = 233970423115425145549737651362517029924. The first gotcha is that the twist is not a cyclic group and just taking small factors of its order will not do (it does have subgroups that are cyclic though). @spdevlin says:
Calculate the order of the twist and find its small factors. This one should have a bunch under 2^24.
Well, the small factors are [2, 11, 107, 197, 1621, 105143, 405373, 2323367]. However you will not be able to find a generator of order 2 if you use assume the twist has a cyclic order of 233970423115425145549737651362517029924. You will be able to find generators for the other small factors: [11, 107, 197, 1621, 105143, 405373, 2323367]. For a randomly generated Bob’s private key, sending the generators of these subgroups disguised as Alice’s public keys reveals the following facts about Bob’s private key b:
Generator of order 11 found: 76600469441198017145391791613091732004
Found b mod 11: 4 or 11-4=7
Generator of order 107 found: 215154098129284057249603159073175023533
Found b mod 107: 24 or 107-24=83
Generator of order 197 found: 94955123407611383099634454718224635806
Found b mod 197: 44 or 197-44=153
Generator of order 1621 found: 90340124320150600231802526508276130439
Found b mod 1621: 390 or 1621-390=1231
Generator of order 105143 found: 226695433509445480278297098756629724558
Found b mod 105143: 6979 or 105143-6979=98164
...
You thus have 27=128 combinations of Bob’s private key modulo the product of the [11, 107, 197, 1621, 105143, 405373, 2323367] moduli. And then you’ll need to take a DLog for each of these combinations to end up with 128 guesses of Bob’s private key. This will probably take a few days to compute on a typical laptop. Can we do better? Yes, it is possible to whittle down the number of combinations to just two with one additional call to Bob. What you need to do is find a generator on the twist curve of order which is the composite of these small moduli. Staying with the above example, it would mean finding a generator of order
r = 11 · 107 · 197 · 1621 · 105143 · 405373 · 2323367 = 37220200115549684379403037
and then initiating a DH exchange with Bob giving him this generator as Alice’s public key. Poor Bob will then calculate a symmetric key (i.e. the mac key in the context of this challenge) by raising this generator to his private key exponent and send his Mac response.
We will then try to calculate 27 different symmetric keys ourselves each based on one of the 27 combinations
of Bob’s private key modulo r = 37220200115549684379403037. Those combinations that
result in the identical Mac to that returned by Bob are the ones that are worth taking a DLog on to recover Bob’s full private key. There’ll
be only two unique candidates of Bob’s private key modulo r = 37220200115549684379403037 to try:
k and 37220200115549684379403037 - k. Initially I had a less elegant way of going about this wrinkle. The current
implementation is thanks to the idea shared with me by Gregory Morse.
I ended up creating a class dedicated to generating different possible values of Bob’s private key
modulo r (i.e. modulo 11 · 107 · 197 · 1621 · 105143 · 405373 · 2323367 = 37220200115549684379403037).
The class implements [Iterable
There are more intricacies to tackle along the way. Some small, others bigger:
-
A fairly small complication is that finding
b mod small-primerequires ploughing through large ranges for the bigger subgroups. For example to find b mod 2323367 requires wading through the [0, 2323367/2] range, and for each element of the range you need to calculate a DH key and derive a MAC. Without parallelizing this easily take a few minutes. I implemented logic to carry such scans in parallel to save time. -
Once you know Bob’s private key
bmodulo the product of small primesr= 37220200115549684379403037 (b mod r = n), taking a DLog in E(GF(p)) to recover the full private ket will take a few hours of time. The largerr, the less effort DLog will take. Are there any other small factors to use? I searched up to 232 and didn’t find any. However there’s a small improvement possible. Remember that the order of the twist has a divisor of 2 but that you cannot find a subgroup of order 2 if you assume the twist is a cyclic group of order 233970423115425145549737651362517029924? The smallest subgroup you’ll find has order 11. However you can find a subgroup of order 22. So instead of finding residues of Bob’s private key modulo these primes [11, 107, 197, 1621, 105143, 405373, 2323367] I switched to searching for residues of moduli [22, 107, 197, 1621, 105143, 405373, 2323367] instead. Garner’s algorithm still works fine as its only requirement is that moduli be pairwise co-prime. This let me learn Bob’s key modulor= 74440400231099368758806074 instead of modulo 37220200115549684379403037, roughly halving the time needed to take DLog later on.A still cleaner way to address this would be to spend more time analyzing the twist and figuring out the order of its largest cyclic group, which is obviously less than the order of the twist 233970423115425145549737651362517029924. And then search for generators of small subgroups relative to this cyclic subgroup. This challenge reveals an interesting fact — the twist of a cyclic Elliptic Curve group need not be cyclic.
-
Applying the the kangaroo attack from Challenge 58 correctly also warrants a couple of explanations. If Bob’s private key is the same number of bits as the legit generator of the curve, you might easily trip up. In this problem the generator is
MontgomeryECGroup.ECGroupElement(u=4, v=85518893674295321206118380980485522083, order=29246302889428143187362802287225875743)I implemented Bob’s part so that it ensures that its private key has the same number of bits as the generator. By now we know Bob’s private key
bmodris equaln. That means that b = n + m·r and the only thing we miss to reconstruct Bob’s pkbis findingm. Applying the maths of the kangaroo attack from Challenge 58:y = g^b = g^(n + m·r) y = g^n · g^(m·r) y' = y · g^-n = g^(m·r) g' = g^r y' = (g')^mshows that we have everything needed to calculate
mexcept fory, which is Bob’s public key (typically designated as B). How do we findy? It is returned by Bob in every DH response it sends back including the last one we received when we searched for the generator of the subgroup of order 74440400231099368758806074. Here’s a relevant piece of server-side code representing Bob, with an appropriate comment added.public Set8.Challenge60ECDHBobResponse initiate(ECGroupElement g, BigInteger q, BigInteger xA) { init(g, q); macKey = Set8.generateSymmetricKey(g.group(), xA, privateKey, 32, Set8.MAC_ALGORITHM_NAME); mac.init(macKey); return new Set8.Challenge60ECDHBobResponse(g.ladder(privateKey), // this is Bob's public key Set8.CHALLENGE56_MSG, mac.doFinal(Set8.CHALLENGE56_MSG.getBytes()) ); }Now we can do the rest:
ECGroupElement gPrime = base.scale(r), y = base.group().createPoint(resp.xB, base.group().mapToY(resp.xB)); List<BigInteger> ret = new ArrayList<>(); for (BigInteger n : cands) { System.out.printf("Trying b mod %d = %d as Bob's private key%n", r, n); ECGroupElement yPrime = y.combine(base.scale(order.subtract(n))); BigInteger m = gPrime.dlog(yPrime, order.subtract(ONE).divide(r), ECGroupElement::f); n = n.add(m.multiply(r)); ret.add(n); System.out.println("Possible private key: " + n); }
Time for the final run of the test:
@ParameterizedTest @ValueSource(strings = { "rmi://localhost/ECDiffieHellmanBobService" })
void challenge60(String bobUrl) throws RemoteException, ... {
MontgomeryECGroup mgroup = new MontgomeryECGroup(new BigInteger("233970423115425145524320034830162017933"),
valueOf(534), ONE, new BigInteger("233970423115425145498902418297807005944"));
MontgomeryECGroup.ECGroupElement mbase = mgroup.createPoint( // The base point, aka the generator
valueOf(4), new BigInteger("85518893674295321206118380980485522083"));
BigInteger q = new BigInteger("29246302889428143187362802287225875743"); // Order of the base point.
ECDiffieHellman ecBob = (ECDiffieHellman) Naming.lookup(bobUrl);
boolean recovered = false;
for (BigInteger b : breakChallenge60(mbase, q, bobUrl)) {
boolean isValid = ecBob.isValidPrivateKey(b);
System.out.printf("Recovered Bob's secret key: %d? %b%n", b, isValid);
recovered |= isValid;
}
assertTrue(recovered, "Didn't succeed in recovering Bob's secret key :-(");
}
Recall that we have two candidates of Bob’s private key modulo 74440400231099368758806074:
Trying b mod 74440400231099368758806074 = 23977054913240415887527048 as Bob's private key
k=26, N=11184810
xt=28871456718421, upperBound=29264338846924
yt=MontgomeryECGroup.ECGroupElement(u=66018503796393609535400154879727009901, v=75220517950417414937371017845721779515)
Possible private key: 28218217810951813013557371685215994592
Trying b mod 74440400231099368758806074 = 50463345317858952871279026 as Bob's private key
k=26, N=11184810
xt=28871456718421, upperBound=29264338846924
yt=MontgomeryECGroup.ECGroupElement(u=66018503796393609535400154879727009901, v=75220517950417414937371017845721779515)
Possible private key: 50463345317858952871279026
Recovered Bob's secret key: 28218217810951813013557371685215994592? true
Recovered Bob's secret key: 50463345317858952871279026? false
This challenge is an excellent demonstration of the extra safety that one obtains by using only the x-coordinates of Alice’s and Bob’s public keys when implementing DH on an elliptic curve group. If Alice and Bob go a step further and also ensure that they use a twist secure elliptic curve group E(GF(p)) such as the curve 25519, their implementation will be almost bullet-proof. E.g. a twist secure elliptic curve group is one whose quadratic twist Ē(GF(p)) has a prime order or an order without any small subgroups. The challenge also highlights the importance of choosing large private keys, ideally the same number of bits as the order of the generator.
Challenge 61. Duplicate-Signature Key Selection in ECDSA (and RSA)
The first part of Challenge 61 that concerns itself with Duplicate Signature Key Selection (DSKS) for ECDSA is almost trivial compared to anything else in Sets 7 and 8. The implementation is quite compact and simpler than DSA atop of Zp* since there’s only one cyclic group of points on E(Fp) to deal with rather than two groups Zp* and Zq* as is the case in the classical DSA. The effort to produce a DSKS for ECDSA is negligible, even for an industry standard curve such as the curve 25519:
@Test
void challenge61ECDSA() {
MontgomeryECGroup curve25519 = new MontgomeryECGroup(CURVE_25519_PRIME,
valueOf(486662), ONE, CURVE_25519_ORDER.shiftRight(3), CURVE_25519_ORDER);
MontgomeryECGroup.ECGroupElement curve25519Base = curve25519.createPoint(
valueOf(9), curve25519.mapToY(valueOf(9)));
BigInteger q = curve25519.getCyclicOrder();
ECDSA ecdsa = new ECDSA(curve25519Base, q);
DSAHelper.Signature signature = ecdsa.sign(CHALLENGE56_MSG.getBytes());
ECDSA.PublicKey legitPk = ecdsa.getPublicKey(),
forgedPk = Set8.breakChallenge61ECDSA(CHALLENGE56_MSG.getBytes(), signature, ecdsa.getPublicKey());
assertTrue(legitPk.verifySignature(CHALLENGE56_MSG.getBytes(), signature));
assertTrue(forgedPk.verifySignature(CHALLENGE56_MSG.getBytes(), signature));
assertNotEquals(legitPk, forgedPk);
// ECDSA is not strongly secure, i.e. if (r, s) is a valid ECDSA signature on m, then so is (r, -s).
DSAHelper.Signature altSignature = new DSAHelper.Signature(signature.getR(), q.subtract(signature.getS()));
assertTrue(legitPk.verifySignature(CHALLENGE56_MSG.getBytes(), altSignature));
assertTrue(forgedPk.verifySignature(CHALLENGE56_MSG.getBytes(), altSignature));
}
An important point about ECDSA worth mentioning is that ECDSA signatures are not strongly secure in the sense that
if (r, s) is a valid signature on message m then it is easy to come up with another valid signature on the same message.
For ECDSA that is (r, -s). The last three statements in the above test demonstrate this in action.
Why does signature (r, -s) work too? This is easy to see from how r is constructed:
function sign(m, d):
k := random_scalar(1, n)
r := (k * G).x
s := (H(m) + d*r) * k^-1
return (r, s)
There’s another point on the curve whose x coordinate matches that of k · G, it is point -k · G. Plugging -k · G in the verification formulas shows the desired outcome.
Mounting a DSKS attack on RSA is much more laborious. I implemented it for relatively small RSA moduli of 320 bits.
The biggest effort went into finding primes p and q that meet the requirements for 1) p-1 and q-1 being smooth, 2)
both s and pad(m) (s^e = pad(m) mod N) being generators of the entire Zp* and Zq* groups, and 3) gcd(p-1, q-1)=2.
I used PKCS#1 v1.5 mode 1 padding with SHA-1, just like in Challenge 42.
To remind, PKCS#1 v1.5 mode 1 paddding looks as follows:
0x00 || 0x01 || PS || 0x00 || ASN.1 || HASH
where the padding string PS must consist of at least eight 0xff bytes. Given SHA-1 hashes take up 20 bytes, and ASN.1
designation of SHA-1 another 15, this all leads to a minimum RSA modulus length of 20+15+3+8=46 bytes or 368 bits.
This length of RSA moduli is rather difficult to work with, so I implemented this challenge by allowing the padding string
PS to consist of two rather than 8 0xff bytes. This reduces the overhead of PKCS#1 padding with SHA-1 to
20+15+3+2=40 bytes, implying a minimum RSA modulus of 320 bits.
I ended up writing quite a bit of concurrent code to tackle this, and pre-calculated all small primes less than 220 so as to be able to find primes meeting the criterion 1) above in linear time. Even with such relatively small moduli (both p and q are around 160 bits), finding them takes on the order of 20 minutes on my MacBook Pro with all cores searching. NB it is vital that p*q is larger than the modulus of the original public key, so I search for primes that are 161 bits long to play it safe.
Suitable primes found:
DiffieHellmanUtils.PrimeAndFactors(p=2252226720431925817465020447075111488063403846689, factors=[2, 7, 277, 647, 2039, 2953, 14633, 139123, 479387, 904847]),
DiffieHellmanUtils.PrimeAndFactors(p=2713856776699319359494147955700110393372009838087, factors=[2, 13, 17, 23, 26141, 56633, 80429, 241567, 652429, 1049941])]
After that I calculate ep=logs(pad(m)) mod p and eq=logs(pad(m)) mod q using a combination of
Pohlig-Hellman and J.M. Pollard’s Lambda Method using a technique from Challenge 59.
To make Pollard’s Lambda Method tractable I ensured that the product
of all prime factors for each of p-1 and q-1 is at least 3700000000000000000000000000000000. I arrived at this
number heuristically, for DLogs in a group whose prime is around 160 bits long Pollard’s Lambda Method works reasonably fast.
For smaller moduli I divide it by 20.7·(320 - RSA_Modulus_bit_length).
The following part of the problem description deserves a word of caution
4. Use the Chinese Remainder Theorem to put ep and eq together:
e' = crt([ep, eq], [p-1, q-1]) The reasoning behind this formula is pretty straightforward: we know that s<sup>ep</sup>≡pad(m) mod p and that s<sup>eq</sup>≡pad(m) mod q. Since the computations are in GF(p) and GF(q) by Fermat's theorem this is equivalent to s<sup>ep mod (p-1)</sup>≡pad(m) mod p and s<sup>eq mod (q-1)</sup>≡pad(m) mod q. Thus we need to find e such that e ≡ ep mod (p-1) and e ≡ eq mod (q-1). However plugging it into the CRT formula
e = ( ((ep−eq) ((q-1)−1 mod (p-1) )) mod (p-1) )·(q-1) + eq
will fail because (q-1) is not invertible mod (p-1) as they are both even. I used the approach delineated in Section 4.1 of this paper to correctly tackle it.
One interesting nuance that @spdevlin doesn’t explain is why the forged e is a valid RSA exponent. We made sure that
we found two suitable smooth primes p and q. You will recall that one of the conditions for candidate primes was
that both s and pad(m) be generators of the entire Zp* and Zq* groups
(i.e. that they are both primitive roots of Zp* and Zq* respectively):
s shouldn’t be in any subgroup that pad(m) is not in. If it is, the discrete logarithm won’t exist. The simplest thing to do is make sure they’re both primitive roots.
This implies that ep (in s^ep = pad(m) mod p) is relatively prime with p-1 — the order of Zp*.
Analogously eq is relatively prime with q-1. This, in turn, implies that e is relatively prime with (p-1)·(q-1) the order
of group ZN* and hence a valid RSA exponent.
Thwarting DSKS attacks is trivial, the signer needs to attach their public key to the message before signing it. While
the verifier should do an extra check to ensure the public key they use to verify corresponds to the one added
to the message. This way, the signing public key is authenticated along with the message. On top of it, it makes sense
to pay attention to the public keys of RSA and be suspicious of public exponents e that are not among the commonly
used ones: { 3, 5, 17, 65537 }.
The challenge ends with the following invitation:
Since RSA signing and decryption are equivalent operations, you can use this same technique for other surprising results. Try generating a random (or chosen) ciphertext and creating a key to decrypt it to a plaintext of your choice!
I tackled it by:
- Generating an RSA key-pair with a 304-bit modulus. Let’s call the resulting key-pair
legitRsa. - PKCS#1 v1.5 padding the plaintext message
id135: credentials invalidusing mode 2 encryption, as explained in Challenge 47. Let’s call the result of this operationpadm. This will play the role of a legit plaintext. To remind, PKCS#1 v1.5 padding for encryption adds randomness so that padding the same plaintext message twice results in two different pads. - PKCS#1 v1.5 padding the plaintext message
id135: credentials valid!using mode 2 encryption. Let’s call the result of this operationforgedPadm. This will play the role of a forged plaintext. - Encrypting
padmusinglegitRsapublic key. Let’s call the result of this operationcTxt - Searching for an RSA key-pair of approximately the same size as the modulus of
legitRsaand for which the following equation holds: cTxt^forgedD≡forgedPadm (mod forgedN).
WhereforgedDis the private key of the forged RSA key-pair andforgedNis its RSA modulus. This search is done in exactly the same way as for the DSKS attack on RSA earlier in this challenge.
And it all works:
@Test
void challenge61RSAEncryption() {
RSAHelperExt rsa = new RSAHelperExt(RSAHelper.PUBLIC_EXPONENT, 152);
String plainTxt = "id135: credentials invalid", forgedPlainTxt = "id135: credentials valid!";
BigInteger padm = RSAHelperExt.pkcs15Pad(plainTxt.getBytes(), rsa.getPublicKey().getModulus().bitLength()),
cTxt = rsa.encrypt(padm),
forgedPadm = RSAHelperExt.pkcs15Pad(forgedPlainTxt.getBytes(),
rsa.getPublicKey().getModulus().bitLength());
assertArrayEquals(rsa.pkcs15Unpad(rsa.decrypt(cTxt)), plainTxt.getBytes());
RSAHelperExt forgedRsa = Set8.breakChallenge61RSA(forgedPadm, cTxt,
rsa.getPublicKey().getModulus().bitLength(), false);
byte[] pTxt = rsa.pkcs15Unpad(forgedRsa.decrypt(cTxt));
assertArrayEquals(pTxt, forgedPlainTxt.getBytes());
System.out.println("Decrypted ciphertext: " + new String(pTxt) );
}
The unit test passes and outputs:
Decrypted ciphertext: id135: credentials valid!
Challenge 62. Key-Recovery Attacks on ECDSA with Biased Nonces
Challenge 62 is an excellent example of what could happen if a cryptographic
primitive is used incorrectly. It is an egregious misnomer to call the random integer k used in DSA signing a nonce.
A nonce is a number used once. But there’s an important caveat to it — a proper cryptographic algorithm expecting
a nonce should be secure even if an adversary gets to choose its nonces (provided they are all unique, of course).
DSA’s k must be a cryptographically strong (i.e. unpredictable) uniformly distributed random number for the resulting
signing scheme to be secure. I will henceforth put DSA’s nonce in quotation marks to accentuate that it cannot be treated
as a real nonce.
In this attack we get to see what can happen when “nonce” k is biased: its l least significant bits are zero. In this
case all signatures end up sharing the same “nonce” suffix 00000000. To make the attack closer to a real-world setting
I implemented the challenge using curve secp256k1.
This curve is used by Bitcoin, Etherium, and Ripple. The authors of this paper
found multiple cases of signatures with the same key whose “nonces” shared the same suffix. To quote:
256-bit nonces with shared 128-bit suffixes. 121 signatures were compromised by nonces that shared a 128-bit suffix with at least one other signature. 55 of these signatures were used with multisignature addresses and 66 were generated by non-multisignature addresses. 13 keys were compromised this way, which had generated a total of 224 signatures. There were 20 distinct suffixes that had been used by these keys. The earliest signature of this type that we found was from March 2015, and the most recent was from August 2018. Some of the keys were used with nonces that all shared the same suffix, and some were used with nonces of varying and occasionally unique suffixes.
Even though this is much more biased than the 8-bit shared suffixes we get to exploit in this challenge, it still highlights how practical this attack is.
The explanation of the math behind the attack provided by @spdevlin is simply superb. There’s one petty inaccuracy in the problem description: the lattice that needs to be constructed should look like
b1 = [ q 0 0 0 0 0 ... 0 0 0 ]
b2 = [ 0 q 0 0 0 0 ... 0 0 0 ]
b3 = [ 0 0 q 0 0 0 ... 0 0 0 ]
b4 = [ 0 0 0 q 0 0 ... 0 0 0 ]
b5 = [ 0 0 0 0 q 0 ... 0 0 0 ] (1)
b6 = [ 0 0 0 0 0 q ... 0 0 0 ]
... ...
bn = [ 0 0 0 0 0 0 ... q 0 0 ]
bt = [ t1 t2 t3 t4 t5 t6 ... tn ct 0 ]
bu = [ u1 u2 u3 u4 u5 u6 ... un 0 cu ]
and have dimension [n+2 x n+2] (in the problem description it is mistakenly shown to have dimension [n+2 x n+3]).
The main point to fathom is that the vector
bu - d·bt + m1·b1 + m2·b2 + … + mn·bn (2)
is reasonably short and hence is likely to be present in the reduced basis we obtain for our lattice (1). Why is it short? Because early in the problem description we learnt that u - d·t + m·q ~ 0 or less than q/2l to be precise. This means that each element of (2) is less than q/2l and therefore the length of (2) is much shorter than the length of each of the vectors in our original lattice (1).
The implementation of the Gram-Schmidt orthogonalization process and the Lenstra-Lenstra-Lovasz basis reduction algorithm was fairly straightforward. I opted for infinite precision floating point arithmetic provided by Java’s BigDecimal. I created a class with static methods for matrix operations over a field of reals and a simple unit test to verify that the main lattice operations work correctly:
@Test
void matrixOperationsOverFieldOfRealsForChallenge62() {
BigDecimal[][] basis = { { BigDecimal.valueOf(-2), BigDecimal.ZERO, BigDecimal.valueOf(2), BigDecimal.ZERO },
{ BigDecimal.valueOf(.5), BigDecimal.valueOf(-1), BigDecimal.ZERO, BigDecimal.ZERO },
{ BigDecimal.valueOf(-1), BigDecimal.ZERO, BigDecimal.valueOf(-2), BigDecimal.valueOf(.5) },
{ BigDecimal.valueOf(-1), BigDecimal.ONE, BigDecimal.ONE, BigDecimal.valueOf(2) }},
expectedReducedBasis = { { BigDecimal.valueOf(.5), BigDecimal.valueOf(-1), BigDecimal.ZERO, BigDecimal.ZERO },
{ BigDecimal.valueOf(-1), BigDecimal.ZERO, BigDecimal.valueOf(-2), BigDecimal.valueOf(.5) },
{ BigDecimal.valueOf(-.5), BigDecimal.ZERO, BigDecimal.ONE, BigDecimal.valueOf(2) },
{ BigDecimal.valueOf(-1.5), BigDecimal.valueOf(-1), BigDecimal.valueOf(2), BigDecimal.ZERO }},
orthogonalBasis = RealMatrixOperations.gramSchmidt(basis),
reducedBasis = RealMatrixOperations.lLL(basis, BigDecimal.valueOf(.99));
// Is the Gram-Schmidt orthogonalization process implemented correctly?
for (int i=0; i < orthogonalBasis.length; i++) {
for (int j=i+1; j < orthogonalBasis.length; j++) {
assertEquals(0, BigDecimal.ZERO.compareTo( /* The dot product of each pair of distinct vectors must be 0 */
RealMatrixOperations.innerProduct(orthogonalBasis[i], orthogonalBasis[j]).setScale(10, BigDecimal.ROUND_HALF_EVEN)));
}
}
// Is L^3-lattice basis reduction algorithm implemented correctly?
assertTrue(RealMatrixOperations.equals(expectedReducedBasis, reducedBasis));
}
Creating a biased ECDSA signer was trivial too.
One nuance worth pointing out is the number of signatures required to recover the private key. @spdevlin writes:
I get good results with as few as 20 signatures. YMMV.
Well, the actual number of signatures required to assuredly recover the private key will depend on the curve chosen. Since I chose secp256k1 — a pretty advanced secure curve, my mileage turned out to be quite different indeed. I ended up needing 26 messages signed with the same key and different biased nonces. Moreover I had to increase the length of the shared suffix from 8 bits to 12. And, voilà, within half an hour I am able to recover the key:
Extracted private key: 0x59dc17a4bc3b63a7df0b0cde5d58119caa1b2c711ef46fa59735d8f7fe09e9d1
Actual private key: 0x59dc17a4bc3b63a7df0b0cde5d58119caa1b2c711ef46fa59735d8f7fe09e9d1
The code of the main test is pretty compact:
@Test
void challenge62() {
// Using Bitcoin's secp256k1
WeierstrassECGroup secp256k1 = new WeierstrassECGroup(CURVE_SECP256K1_PRIME, ZERO, valueOf(7), CURVE_SECP256K1_ORDER);
BigInteger baseX = new BigInteger("79BE667EF9DCBBAC55A06295CE870B07029BFCDB2DCE28D959F2815B16F81798", 16);
WeierstrassECGroup.ECGroupElement secp256k1Base = secp256k1.createPoint(baseX, secp256k1.mapToY(baseX));
BigInteger q = secp256k1.getCyclicOrder();
// Check whether the curve behaves as expected
assertEquals(secp256k1Base.inverse(), secp256k1Base.scale(q.subtract(ONE)));
assertEquals(secp256k1.getIdentity(), secp256k1Base.scale(q));
assertEquals(secp256k1.getIdentity(), secp256k1Base.combine(secp256k1Base.inverse()));
int l = 12; /* The number of least significant bits in k that will be 0 */
BiasedECDSA ecdsa = new BiasedECDSA(secp256k1Base, q, l);
int numMsgs = 26; // Each call to getPlainText(6) returns random plaintext 2^6 bytes long
BigInteger[][] tuPairs = IntStream.range(0, numMsgs).mapToObj(x -> Set8.getPlainText(6)).map(m -> {
BigInteger[] tuPair = new BigInteger[2];
DSAHelper.Signature sign = ecdsa.sign(m);
// t = r / (s*2^l)
tuPair[0] = sign.getR().multiply(sign.getS().multiply(ONE.shiftLeft(l)).modInverse(q)).mod(q);
// u = H(m) / (-s*2^l)
tuPair[1] = hashAsBigInteger(m).multiply(sign.getS().negate().multiply(ONE.shiftLeft(l)).modInverse(q)).mod(q);
return tuPair;
}).toArray(BigInteger[][]::new);
LatticeAttackHelper helper = new LatticeAttackHelper(tuPairs, q, l);
BigInteger pk = helper.extractKey();
System.out.printf("Extracted private key:\t0x%x%nActual private key:\t\t0x%x%n", pk, ecdsa.getPrivateKey());
assertEquals(ecdsa.getPrivateKey(), pk);
}
Challenge 63. Key-Recovery Attacks on GCM with Repeated Nonces
Challenge 63 consists of six parts:
- Implementing GF(2128) — Polynomial Galois field over GF(2)
- Implementing Galois Counter Mode (GCM) where the earlier devised GF(2128) is used to calculate the one-time-MAC — GMAC
- Implementing a polynomial ring over GF(2128)
- Solving the problem of factoring polynomials
- Realising the actual attack of recovering the authentication key of GMAC provided a nonce was repeated
- Asking yourself a question of what you can do with the recovered authentication key
All in all it is a fairly laborious challenge that took me quite some time to complete. The effort is commensurate to a university coursework. On the other hand it helped me consolidate my understanding of finite fields and polynomial rings like no text book would ever permit.
Implementing GF(2128)
I came up with a fairly straightforward implementation of GF(2128) using Java’s BigInteger. See com.cryptopals.set_8.PolynomialGaloisFieldOverGF2 for details.
Implementing Galois Counter Mode (GCM)
A correct implementation of GCM turned out a bit more tricky to get right. Here are a couple of important nuances to bear in mind:
- When preparing a buffer over which to calculate the GMAC
a0 || a1 || c0 || c1 || c2 || len(AD) || len(C)everything must be encoded using a big-endian ordering. Padding is done with zero bits appended. I found this document from NIST to to be a good reference. - When converting blocks of plain text into elements of GF(2128) and vice versa, the following enjoinder
from @spdevlin is crucial
We can convert a block into a field element trivially; the leftmost bit is the coefficient of x^0, and so on.
At the end all fell into place and I was able to confirm my implementation of the GCM to produce the same results as that from the JRE:
@Test
void GCM() {
KeyGenerator aesKeyGen = KeyGenerator.getInstance("AES");
SecretKey key = aesKeyGen.generateKey();
GCM gcm = new GCM(key);
byte[] nonce = new byte[12], plnText = CHALLENGE56_MSG.getBytes(), cTxt1, cTxt2, assocData = new byte[0];
new SecureRandom().nextBytes(nonce);
cTxt1 = gcm.cipher(plnText, assocData, nonce);
// Confirm that we get the same ciphertext as that obtained from a reference implementation.
Cipher cipher = Cipher.getInstance("AES/GCM/NoPadding");
// Create GCMParameterSpec
GCMParameterSpec gcmParameterSpec = new GCMParameterSpec(16 * 8, nonce);
cipher.init(Cipher.ENCRYPT_MODE, key, gcmParameterSpec);
cTxt2 = cipher.doFinal(plnText);
assertArrayEquals(cTxt2, cTxt1);
// Confirm that decrypting will produce the original plain text
assertArrayEquals(plnText, gcm.decipher(cTxt1, assocData, nonce));
// Confirm that garbling a single byte of cipher text will result in the bottom symbol
cTxt1[0] ^= 0x03;
assertArrayEquals(null, gcm.decipher(cTxt1, assocData, nonce));
}
Implementing a polynomial ring over a finite field
Instead of implementing a polynomial ring over GF(2128) I decided to implement it as a generic class over any finite field:
public interface FiniteFieldElement {
FiniteFieldElement add(FiniteFieldElement e);
FiniteFieldElement subtract(FiniteFieldElement e);
/**
* Computes this + this + ... + this {@code k} times
* @return an object of the implementing class.
*/
FiniteFieldElement times(BigInteger k);
FiniteFieldElement multiply(FiniteFieldElement e);
FiniteFieldElement modInverse();
/**
* Computes this * this * ... * this {@code k} times, i.e. computes this<sup>k</sup>
* @return an object of the implementing class.
*/
FiniteFieldElement scale(BigInteger k);
FiniteFieldElement getAdditiveIdentity();
FiniteFieldElement getMultiplicativeIdentity();
BigInteger getOrder();
BigInteger getCharacteristic();
}
So as to test my implementation of polynomial rings, I wrote a class representing GF(Zp) fields. It is much easier to reason about Zp arithmetic than arithmetic in GF(2128).
Solving the problem of factoring polynomials
This entailed working out:
- Division of polynomials: https://en.wikipedia.org/wiki/Polynomial_long_division#Pseudocode
- Differentiation of polynomials
- GCD for polynomials
- Square-free factorization of polynomials: https://en.wikipedia.org/wiki/Factorization_of_polynomials_over_finite_fields#Square-free_factorization
- Distinct-degree factorization of polynomials: https://en.wikipedia.org/wiki/Factorization_of_polynomials_over_finite_fields#Distinct-degree_factorization
- Equal-degree factorization of polynomials: https://en.wikipedia.org/wiki/Factorization_of_polynomials_over_finite_fields#Equal-degree_factorization
Distinct-degree factorization
Of these problems I spent the most time getting distinct-degree factorization to work. The first obstacle I faced was my earlier decision to represent polynomials as arrays of coefficients. This algorithm requires dealing with polynomials whose degree is the order of the field and higher, which turns out to be 2128 for this field. E.g. a polynomial like this one: x2128 - x = x340282366920938463463374607431768211456 + x in GF(2128). To tackle it I switched to representing polynomials in a way that stores only their non-zero coefficients.
The second obstacle was the awful running time of the Distinct-degree factorization algorithm from Wikipedia. It has a running time of O(q) where q is the order of GF(2128), which takes forever. I tackled it by adopting a Distinct-degree factorization algorithm that uses repeated squaring.
Equal-degree factorization
Equal-degree factorization, while fairly well delineated by @spdevlin, presented a couple of difficulties too. To start
with, calculating
g := h^((q^d - 1)/3) - 1 mod f
as specified in the problem description will take forever for the very same reason as I indicated above —
the order (qd-1)/3 will be too large. You need to raise to this high a power by constantly taking modulus
of f in your exponentiation routine. I solved it by implementing a scaleMod method on my Polynomial Ring class.
The other difficulty is that the square-free polynomial without distinct-degree factors that you pass to your edf implementation might not have factors of the degree you specify. This would lead to the algorithm running ad infinitum… For example in my approach I always call edf with a desired degree of factors being 1. While the setting guarantees the presence of at least one factor of degree 1 for the original polynomial, there’s no guarantee that each polynomial spewed out by distinct-degree factorization can be factoed in one-degee polynomials. I dealt with this predicament by setting a heuristic limit on the maximum number of passes through the loop in my edf implementation. When the polynomial passed to edf has factors of requested degree, this heuristic limit will not halt the loop without finding the factors with a probability close to 1.
// maxPasses ensures the method doesn't hang if this polynomial can't be factored into d-degree polynomials
int maxPasses = 5 * (int) Math.ceil((32 - Integer.numberOfLeadingZeros(r)) * 2.5);
Realising the actual attack of recovering the authentication key
All the hard work on implementing square-free factorization, distinct-degree factorization, end equal-degree factorization can finally be brought to bear:
KeyGenerator aesKeyGen = KeyGenerator.getInstance("AES");
SecretKey key = aesKeyGen.generateKey();
GCM gcm = new GCM(key);
byte[] nonce = new byte[12], plnText = "crazy flamboyant for the rap enjoyment".getBytes(),
plnText2 = "dummy text to try".getBytes(),
cTxt1, cTxt2, assocData = "valid assoc.Data".getBytes();
new SecureRandom().nextBytes(nonce);
// a0 || a1 || c0 || c1 || c2 || (len(AD) || len(C)) || t
cTxt1 = gcm.cipher(plnText, assocData, nonce);
// Reusing the same nonce, thereby making ourselves vulnerable to the attack.
cTxt2 = gcm.cipher(plnText2, assocData, nonce);
PolynomialRing2<PolynomialGaloisFieldOverGF2.FieldElement> poly1 = GCM.toPolynomialRing2(cTxt1, assocData),
poly2 = GCM.toPolynomialRing2(cTxt2, assocData),
equation = poly1.add(poly2).toMonicPolynomial();
System.out.println("cTxt1 polynomial: " + poly1);
System.out.println("cTxt2 polynomial: " + poly2);
System.out.println("Equation: " + equation);
List<PolynomialRing2<PolynomialGaloisFieldOverGF2.FieldElement>>
allFactors = equation.squareFreeFactorization().stream().map(PolynomialRing2.PolynomialAndPower::getFactor)
.flatMap(x -> x.distinctDegreeFactorization().stream()).collect(Collectors.toList()),
oneDegreeFactors = allFactors.stream().filter(x -> x.intDegree() == 1).collect(Collectors.toList()),
oneDegreeFactorsThroughEdf = allFactors.stream().filter(x -> x.intDegree() > 1)
.flatMap(x -> x.equalDegreeFactorization(1).stream()).collect(Collectors.toList());
System.out.println("Actual authentication key: " + gcm.getAuthenticationKey());
System.out.println("Candidates found after distinct-degree factorization: " + oneDegreeFactors);
System.out.println("Additional candidates found after equal-degree factorization: " + oneDegreeFactorsThroughEdf);
oneDegreeFactors.addAll(oneDegreeFactorsThroughEdf);
List<PolynomialGaloisFieldOverGF2.FieldElement> candidateAuthenticationKeys =
oneDegreeFactors.stream().map(x -> x.getCoef(0)).collect(Collectors.toList());
assertTrue(candidateAuthenticationKeys.contains(gcm.getAuthenticationKey()));
Running it produces the following output:
cTxt1 polynomial: 862e862274c6f6cece8604269636866ex^5 + a2c92e99dba07ce117b3bb3665fedff9x^4 + f4551f6d035a339b2e5b061ca2830ce4x^3 + 320f10f267edx^2 + c800000000000000100000000000000x + 5aafa98bf7b25cfe22f5e630f97d59e9
cTxt2 polynomial: 862e862274c6f6cece8604269636866ex^4 + c291acf103e2e47987fbbb368dce3f19x^3 + 7ex^2 + 11000000000000000100000000000000x + b3180499d9b2e60566ac9c204aad7ff
Equation: x^5 + 597419e85ea532a59c4d0eed034a9044x^4 + 812f7801991ead15d455a70fcb83086fx^3 + 87c24da8d5f25ea3e9f92b8c9b319712x^2 + 10ec19974d245b5f16890e6a1effeec8x + e4cb0203ef19430f3c13947f6f6d17a7
Actual authentication key: 67cf01239432c85151d9f7c021bfd121
Candidates found after square-free and distinct-degree factorization: []
Additional candidates found after equal-degree factorization: [x + 67cf01239432c85151d9f7c021bfd121, x + e8cde43205a09d05379422572e11dfb5]
Asking yourself a question of what you can do with the recovered authentication key
Having gone to the lengths of completing this Herculean labour of recovering the GMAC authentication key from a victim who naively encrypted two different plain texts with the same nonce, you might wonder what you can do with it. Well, you can forge a piece of distinct cipher text that the cryptosystem you attack will authenticate. In other words you can mount an existential forgery attack.
Imagine that t0 is the last block of the first cipher text you have cTxt1. Looking at the way it was calculated
t0 = a0*h^5 + c0*h^4 + c1*h^3 + c2*h^2 + l0*h + s
and noting that you have both a0 and h, you can go far. Say a'0 is a block of your bogus associated data you want to swap for
the legitimate block a0. What you do is first subtract a0*h^5 from t0 and then replace it with a block of bogus
associated data by adding a'0*h^5 to t0. Here’s how it looks in my code:
/**
* Forges valid cipher text from legit cipher text and associated data coupled with a recovered authentication key.
* @param additionalBogusAssocData blocksize-long buffer, must be the same size as padded {@code legitAssocData}
*/
public static byte[] forgeCipherText(byte[] legitCipherText, byte[] legitAssocData, byte[] additionalBogusAssocData,
PolynomialGaloisFieldOverGF2.FieldElement authenticationKey) {
int plainTextLen = legitCipherText.length - BLOCK_SIZE,
assocDataPaddedLen = (legitAssocData.length / BLOCK_SIZE + (legitAssocData.length % BLOCK_SIZE != 0 ? 1 : 0)) * BLOCK_SIZE,
plainTextPaddedLen = (plainTextLen / BLOCK_SIZE + (plainTextLen % BLOCK_SIZE != 0 ? 1 : 0)) * BLOCK_SIZE,
lastPower = plainTextPaddedLen / BLOCK_SIZE + 1,
last = additionalBogusAssocData.length / BLOCK_SIZE;
if (additionalBogusAssocData.length != assocDataPaddedLen) {
throw new IllegalArgumentException("additionalBogusAssocData must be of same length as padded legit associated data and not "
+ additionalBogusAssocData.length);
}
// We start with the original legit tag...
PolynomialGaloisFieldOverGF2.FieldElement forgedTag = toFE(Arrays.copyOfRange(
legitCipherText, legitCipherText.length - BLOCK_SIZE, legitCipherText.length));
byte[] buf = new byte[assocDataPaddedLen];
System.arraycopy(legitAssocData, 0, buf, 0, legitAssocData.length);
// ... and then subtract from it the legit associated data and
// add to it bogus associated data.
for (int i=last; i > 0; i-=1) {
lastPower++;
// Remove the summand of the legit associated data
forgedTag = forgedTag.subtract(
toFE( Arrays.copyOfRange(legitAssocData, (last - 1) * BLOCK_SIZE, last * BLOCK_SIZE))
.multiply(authenticationKey.scale(valueOf(lastPower))) );
// And then add the summand of the bogus associate data
forgedTag = forgedTag.add(
toFE( Arrays.copyOfRange(additionalBogusAssocData, (last - 1) * BLOCK_SIZE, last * BLOCK_SIZE))
.multiply(authenticationKey.scale(valueOf(lastPower))) );
}
byte[] res = legitCipherText.clone();
System.arraycopy(forgedTag.asArray(), 0, res, legitCipherText.length - BLOCK_SIZE, BLOCK_SIZE);
return res;
}
Giving it a spin:
cTxt1 polynomial: 862e862274c6f6cece8604269636866ex^5 + a2c92e99dba07ce117b3bb3665fedff9x^4 + f4551f6d035a339b2e5b061ca2830ce4x^3 + 320f10f267edx^2 + c800000000000000100000000000000x + 5aafa98bf7b25cfe22f5e630f97d59e9
cTxt2 polynomial: 862e862274c6f6cece8604269636866ex^4 + c291acf103e2e47987fbbb368dce3f19x^3 + 7ex^2 + 11000000000000000100000000000000x + b3180499d9b2e60566ac9c204aad7ff
Equation: x^5 + 597419e85ea532a59c4d0eed034a9044x^4 + 812f7801991ead15d455a70fcb83086fx^3 + 87c24da8d5f25ea3e9f92b8c9b319712x^2 + 10ec19974d245b5f16890e6a1effeec8x + e4cb0203ef19430f3c13947f6f6d17a7
Actual authentication key: 67cf01239432c85151d9f7c021bfd121
Candidates found after square-free and distinct-degree factorization: []
Additional candidates found after equal-degree factorization: [x + 67cf01239432c85151d9f7c021bfd121, x + e8cde43205a09d05379422572e11dfb5]
Recovered authentication key: 67cf01239432c85151d9f7c021bfd121
Legit associated data: valid assoc.Data
Bogus associated data: bogus assoc.Data
Legit cipher text: 9FFB7FA66CDDCDE8873E05DB997493452730C1453860DA74D9CC5AC0B6F8AA2FB7E64F08F04C979ABE9F0C67AF447F3A4DEFD195F55A
Forged cipher text: 9FFB7FA66CDDCDE8873E05DB997493452730C1453860DA74D9CC5AC0B6F8AA2FB7E64F08F04CDE9E643787D35A6765241FEC4324627A
Decrypted by the crypto system under attack into: crazy flamboyant for the rap enjoyment
Recovered authentication key: e8cde43205a09d05379422572e11dfb5
Legit associated data: valid assoc.Data
Bogus associated data: bogus assoc.Data
Legit cipher text: 9FFB7FA66CDDCDE8873E05DB997493452730C1453860DA74D9CC5AC0B6F8AA2FB7E64F08F04C979ABE9F0C67AF447F3A4DEFD195F55A
Forged cipher text: 9FFB7FA66CDDCDE8873E05DB997493452730C1453860DA74D9CC5AC0B6F8AA2FB7E64F08F04CD3355D1A58A0B6E730F4356A7027481F
Decrypted by the crypto system under attack into: ⊥
I am able to commit an existential forgery attack!
Challenge 64. Key-Recovery Attacks on GCM with a Truncated MAC
Challenge 64 implements an attack first outlined by Niels Ferguson in his Authentication weaknesses in GCM paper. GCM is the most popular standard for authenticated encryption and is used in TLS 1.2 and higher. To aid efficient fast implementations of GCM Intel even added a special new instruction PCLMULQDQ, which makes it easy to implement GCM’s GHASH hash function. Of the different modes of authenticated encryption not encumbered by patents and certified by NIST, GCM is the fastest. It is faster than CCM and EAX. Moreover, with the help of Intel’s PCLMULQDQ instruction for GHASH, it can be implemented with less code than would otherwise be required. All of these are the main reasons for GCM’s popularity.
Niels’s paper shows that the actual authentication security of GCM will be less than the number of bits in its authentication tag.
Given the maximum tag size of 128 bits, the best possible authentication security of GCM can be 128 - k bits where k
is ⌊log2(number-of-blocks-encrypted)⌋. Niels’s paper shows that for smaller authentication tag
sizes, it will be worse than n - k bits because of some peculiarities of the GHASH one-time hash function that GCM uses.
Like Challenge 63, this challenge shows how to succeed at an existential forgery attack on GCM. This time without your adversary having made any mistakes in using GCM apart from choosing a small authentication tag size. Namely the minimum size allowed for GCM’s authentication tag by NIST of 32 bits.
To tackle this challenge you will need to implement the following parts.
- Linear algebra routines for GF(2) and GF(2128):
- Implementing a vector representation for elements of GF(2128);
- Implementing a matrix representation for multiplication by a constant in GF(2128) and for squaring in GF(2128);
- Implementing basic operations for matrices in GF(2): addition, multiplication, scaling, transposition, Gaussian elimination, finding a kernel.
- Extraction and replacement of 2i-th blocks of ciphertext counting from the end, i.e. all blocks of the ciphertext that are the coefficients of x2^i (where i = 1, 2, …, n) in the GHASH polynomial in the indeterminate x over GF(2128).
- Calculation of matrix Ad = ∑MDi(MS)i, where MDi are matrix representations of the differences between the 2i-th element of ciphertext and its forged counterpart. Along with the calculation of the dependency matrix T, as explained in the challenge.
- Finding the kernel of the matrix T, whose elements represent all the possible manipulations to the 2i-th blocks of ciphertext that don’t change the most significant 16 bits of GHASH.
- Attempting an existential forgery attack on the smallest allowed GHASH tag size of 32 bits.
- Recovering the authentication key.
Linear algebra
Implementing a vector representation for elements of GF(2128)
I added two new methods to my class for representing GF(2128) elements: PolynomialGaloisFieldOverGF2::FieldElement::asVector and PolynomialGaloisFieldOverGF2::createElement
Implementing a matrix representation for multiplication by a constant and for squaring
Analogously to vector representation, I wrote these as methods of my class for GF(2128): PolynomialGaloisFieldOverGF2::FieldElement::asMatrix and PolynomialGaloisFieldOverGF2::getSquaringMatrix
Implementing basic operations for matrices in GF(2)
I felt it would be an overkill to create a whole new class to represent matrices over GF(2), instead I went for
a simple representation as boolean[][] and the BooleanMatrixOperations class
with static methods that accept matrices and vectors in GF(2).
Time for some tests to validate that everything works correctly:
@DisplayName("Linear algebra over GF(2)") @Test
void linearAlgebraForChallenge64() {
BigInteger modulus = ONE.shiftLeft(128).or(valueOf(135));
PolynomialGaloisFieldOverGF2 gf = new PolynomialGaloisFieldOverGF2(modulus);
PolynomialGaloisFieldOverGF2.FieldElement c = gf.createElement(valueOf(3)), y = gf.createElement(valueOf(15));
assertEquals(c.multiply(y), gf.createElement(multiply(c.asMatrix(), y.asVector())) );
assertEquals(y.multiply(y), gf.createElement(multiply(gf.getSquaringMatrix(), y.asVector())) );
assertEquals(c, gf.createElement(multiply(c.asMatrix(), gf.getMultiplicativeIdentity().asVector())) );
assertEquals(y, gf.createElement(y.asVector()));
boolean[][][] mss = new boolean[18][][];
mss[0] = gf.getSquaringMatrix();
for (int i=1; i < 18; i++) {
mss[i] = multiply(mss[i-1], mss[0]);
}
assertEquals(y.scale(valueOf(2)), gf.createElement(multiply(mss[0], y.asVector()) ));
assertEquals(y.scale(valueOf(4)), gf.createElement(multiply(mss[1], y.asVector()) ));
assertEquals(y.scale(valueOf(8)), gf.createElement(multiply(mss[2], y.asVector()) ));
assertEquals(y.scale(valueOf(16)), gf.createElement(multiply(mss[3], y.asVector()) ));
// Mc * Ms^i * y) = c * y^4
assertEquals(c.multiply(y.scale(valueOf(16))),
gf.createElement(multiply(multiply(c.asMatrix(), mss[3]), y.asVector())) );
// Confirm matrix representation of GHASH works correctly
PolynomialGaloisFieldOverGF2.FieldElement c1 = gf.createRandomElement(), c2 = gf.createRandomElement(),
c4 = gf.createRandomElement(), c8 = gf.createRandomElement(), h = gf.createRandomElement(), tag1, tag2;
// t = c1*h + c2*h^2 + c4*h^4 + c8*h^8
// First calculate the tag using plain GF(2^128)
tag1 = c1.multiply(h).add(c2.multiply(h.scale(valueOf(2)))).add(c4.multiply(h.scale(valueOf(4)))).add(c8.multiply(h.scale(valueOf(8))));
// Then do the same using a matrix-based representation of GF(2^128) operations
tag2 = gf.createElement(multiply(add(add(add(c1.asMatrix(), multiply(c2.asMatrix(), mss[0])), multiply(c4.asMatrix(), mss[1])), multiply(c8.asMatrix(), mss[2])), h.asVector()));
assertEquals(tag1, tag2);
}
Gaussian elimination is a little trickier. I started with an algorithm on Wikipedia and adapted it for GF(2). A similar algorithm, albeit with a small omission, can be found in this paper. The result is this static method.
The hardest part is finding the kernel of a matrix. I made use of this algorithm from Wikipedia, which is essentially the same as given by @spdevlin in the problem description:
Finding a basis for the null space is not too hard. What you want to do is transpose T (i.e. flip it across its diagonal) and find the reduced row echelon form using Gaussian elimination. Now perform the same operations on an identity matrix of size n*128. The rows that correspond to the zero rows in the reduced row echelon form of T transpose form a basis for N(T).
My implementation is captured in this method.
Extraction and replacement of the 2i-th blocks of ciphertext
This is the easiest part. The only thing to pay attention to is that the blocks to extract are the coefficients of h2^i (where i = 1, 2, …, n) in the polynomial in the indeterminate h over GF(2128): t = s + c1·h + c2·h2 + c3·h3 + … + cn·hn. c2 is the last block of the ciphertext before the tag, and cn is the first (assuming that the plain text was 2n blocks long).
For efficiency’s sake I convert the extracted coefficients into elements of GF(2128). The relevant code is here: extraction of coefficients, replacement of coefficients.
Calculation of matrix Ad = ∑MDi(MS)i and a dependency matrix
With the routines for linear algebra described in the beginning of this section calculating Ad is trivial. Still a good test is in order to gain confidence before going further:
// Generate random coefficients to replace the legit ones for h<sup>2^i</sup> (i=1..17)
coeffsPrime = h.getRandomPowerOf2Blocks();
// Confirm that ad is calculated correctly
boolean[][] ad = h.calculateAd(coeffsPrime);
PolynomialGaloisFieldOverGF2.FieldElement hash1 = gcm.ghashPower2BlocksDifferences(h.getPowerOf2Blocks(), coeffsPrime),
hash2 = coeffs[0].group().createElement(multiply(ad, gcm.getAuthenticationKey().asVector()));
assertEquals(hash1, hash2);
As you can see, I calculate the hash1 over di differences using standard GHASH arithmetic in GF(2128) and then hash2 by Ad·h. TThe two must be the same.
The dependency matrix is more involved. Before setting out on a path to calculate it, it helps to understand what purpose it serves and how it comes about. In his original description of the attack Niels Ferguson writes:
It is now easy to force bits of the error polynomial to zero. Write equations setting each of the bits in a single row of AD to zero. Each equation imposes a single linear constraint on the choice we have for the bits of the Di values. To force a single result bit to zero we have to create 128 linear constraints. If we have n different Di coefficients to choose, we have 128 · n free variables and we can force n − 1 bits of the result to zero.
The depdendency matrix is the Ai,j coefficients of these equations. Here’s how the dependency matrix looks:
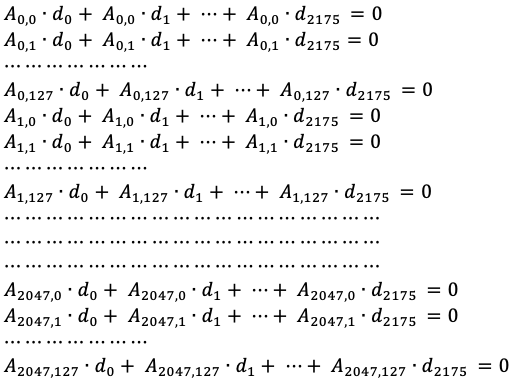
To calculate it you first need to generate arbitrary coefficients of h2^i (i=1..17). They are the starting point for deriving properly forged coefficients. There will be exactly 17·128=2176 bits that you can flip, 128 per each coefficient. In the above equations they are denoted with d0, d1, …, d2175. The way you then calculate the dependency matrix — all the different Ai,j in the above equations — is precisely as described by @spdevlin:
Iterate over the columns. Build the hypothetical Ad you’d get by flipping only the corresponding bit. Iterate over the first (n-1)*128 cells of Ad and set the corresponding cells in this column of T.
So you flip d0 in the coefficient of h2 that you just generated and then calculate Ad over your generated coefficients. The first 16·128 cells of this Ad constitute the values of the first column of the dependency matrix being generated.
For the sake of efficiency I decided to generated a transpose of the dependency matrix. This will make the calculation of its kernel faster.
Since in this problem we repeatedly touch on the notion of the kernel (aka the null space), it’s worth saying a couple of words about the linear algebra used. Let’s start with @spdevlin’s explanation:
If you know a little bit of linear algebra, you’ll know that what we really want to find is a basis for N(T), the null space of T. The null space is exactly that set of vectors that solve the equation above. Just what we’re looking for. Recall that a basis is a minimal set of vectors whose linear combinations span the whole space.
In linear algebra a matrix T of dimensions [m x n] defines a mapping from n-dimensional column vectors to m-dimensional ones.
So we have two vector spaces one of dimension n and another of dimension m (both over field GF(2) in this problem) and a mapping T
from one vector space to the other. The kernel of this mapping T are the pre-images (elements from the n-dimensional vector space) that get mapped
to the zero vector from the m-dimensional vector space. Looking at the above-mentioned dependency matrix of dimension [2048 x 2176],
we are dealing with two vector spaces over GF(2): one of dimension 2176 and the other of dimension 2048. And then we identify
those elements of the first vector space that get mapped by T to the zero vector from the second vector space. Since
the first vector space is of a larger dimension than the second, the mapping T is a many-to-one mapping (by pigeonhole principle).
Therefore we should expect to find multiple such vectors.
Finding the kernel of the dependency matrix T
With the dependency matrix generated we can now start looking for what flips to the different bits of these prototype coefficients are required so that the first 16 rows of Ad are zeros. This is trivial to do with the kernel function that I outlined in an earlier section. For the sake of efficiency I implemented an optimized version called kernelOfTransposed that finds the kernel from a transposed dependency matrix. NB: In contrast to the problem description:
Finding a basis for the null space is not too hard. What you want to do is transpose T (i.e. flip it across its diagonal) and find the reduced row echelon form using Gaussian elimination.
it is sufficient to bring the transpose of T to a row echelon form, there’s no need to bring it to reduced row echelon form.
If everything has been implemented correctly, the equality d · TT = 0 will hold for all elements of the kernel found:
forgedCoeffs = getRandomPowerOf2Blocks();
boolean[][] tTransposed = produceDependencyMatrixTransposed();
kernel = kernelOfTransposed(tTransposed);
// If the kernel was calculated correctly, for each element d of the kernel the product d * tTransposed = 0.
boolean[] expectedProduct = new boolean[tTransposed[0].length], product;
System.out.println("Extracted kernel length: " + kernel.length);
for (boolean[] d : kernel) {
product = multiply(d, tTransposed);
assert Arrays.equals(product, expectedProduct);
}
Attempting an existential forgery attack on the smallest allowed GHASH tag size of tLen = 32 bits
This is by far the most interesting and gratifying part of the exercise where all the earlier building blocks come together. I start with generating random bytes of plaintext. How long should the plaintext be to mount an existential forgery on GHASH with a 32 bit tag? Ideally it should be 233 blocks long. This will however be too much, namely 128 GiB. So we will need to go for 217 blocks, which is 2 MiB, this will let us assuredly zero out 16 bits of ciphertext differnces. We then expect to zero out another 16 bits by trial and error. As Niels puts it:
This, in turn, ensures us that the first 16 bits of the authentication tag will not change if we apply the differences Di to the ciphertext. With only 16 effective authentication bits left, we have a 2−16 chance of a successful forgery. This is a much higher chance than one would reasonably expect from a 32-bit authentication code.
How many tries will be required? Since we will try only those ciphertexts whose GHASH doesn’t differ from the original in 16 bits, the probability that a singly try will result in 32 bits of GHASH being the same as in the GHASH of the original legit ciphertext is: 296/2112=2-16. We will then on average require 65536 tries. NB: The birthday paradox is of no application here as we are not looking for a GHASH match between two arbitrary ciphertext messages!
Having generated 217 blocks of plaintext, I generate a new 128 bit key and a new 96 bit nonce. Then I go ahead to encrypt with GCM. Initially I wanted to use the standard GCM implementation available in the JRE (the default SunJCE provider). I was immediately in for a pleasant surprise. Running the following code
Cipher cipher = Cipher.getInstance("AES/GCM/NoPadding");
GCMParameterSpec gcmParameterSpec = new GCMParameterSpec(4 * 8, nonce);
cipher.init(Cipher.ENCRYPT_MODE, key, gcmParameterSpec);
cTxt1 = cipher.doFinal(plainnText);
leads to java.security.InvalidAlgorithmParameterException: Unsupported TLen value; must be one of {128, 120, 112, 104, 96}.
Clearly Niels’s attack is not possible if one uses standard JRE’s crypto libraries. Therefore to proceed I needed to adapt my implementation
of GCM from Challenge 63 to support different GHASH tag lengths starting from 32 bits, this was trivial. You just need
to make use of the first tLen/4 bytes of the resultant 16 byte tag calculated as GHASH(h) ^ E(K, nonce || 1).
The hunt for a forged ciphertext that passes the oracle then proceeded as follows:
boolean[] expectedBits = new boolean[tLen/2], requiredBits = new boolean[tLen], tag;
int count = 0;
EXIST_FORGERY_FOUND:
while (true) {
for (int i=0; i < h.getKernel().length; i++) {
coeffsPrime = h.forgePowerOf2Blocks(i);
// The majority of d's that we extract from the kernel will zero out the tLen/2 low-order
// bits of GHASH, however we need to rely on trial and error to get all tLen low-order bits
// to be zero.
tag = gcm.ghashPower2BlocksDifferences(coeffs, coeffsPrime).asVector();
// Check if the first tLen/2 bits of the tag are indeed zero. For some reason this test passes for
// about half the elements of the kernel.
if (Arrays.equals(Arrays.copyOf(tag, expectedBits.length), expectedBits)) {
// Only counting as attempts when we correctly zeroed out the leftmost tLen/2 bits.
System.out.printf(" Attempt %4d%n", ++count);
} else continue;
if (!Arrays.equals(Arrays.copyOf(tag, requiredBits.length), requiredBits)) continue;
cTxt2 = GCM.replacePowerOf2Blocks(cTxt1, plainText.length, coeffsPrime);
pTxt2 = gcm.decipher(cTxt2, assocData, nonce);
count++;
System.out.printf("Trying an existential forgery: %s%n", pTxt2 == null ? "\u22A5" : new String(gcm.decipher(cTxt2, assocData, nonce), 0, 1024));
if (pTxt2 != null) break EXIST_FORGERY_FOUND;
}
h.replaceBasis();
}
assertFalse(Arrays.equals(plainText, pTxt2));
Every iteration of the outer loop starts with a new set of forged coefficients, calculating a dependency matrix out of them, and finding the kernel. This is taken care of in the replaceBasis method. Every kernel has 128 vectors. Each vector represents bit flips in the forged coefficients that should make the resulting Ad to have zeros in its first 16 rows (and therefore the 16 first bits of the error polynomial will be zero as well). To remind, the error polynomial is e = ∑MDi·(MS)i·h=Ad·h, where h is the authentication key. About half the vectors in the kernel, when applied to the prototype forged coefficients, indeed zero out the first 16 rows of Ad (and thus guarantee that the first 16 bits of the error polynomial are zeros). Why only half I haven’t yet figured out. Probably because not all equations captured in the dependency matrix T are linearly independent.
A typical run. About half the elements of the found kernel don’t zero out the 16 bits:
Error polynomial: feb42cec84ce141fbe7f1fdcdff01e53.
Error polynomial: fa6bb27bfbebf0d86940b28fe6801e53.
Error polynomial: a83bef2a2213589ad38e6b9d9ce50000. Attempt 23505
Error polynomial: 52ec1f1cf3e01b12040879cd2d040000. Attempt 23506
Error polynomial: c6a96c7813ac59a3f8d0c6b3c1811e53.
Error polynomial: ed73f0efaf893510db8ae87be1bd1e53.
Error polynomial: 1cbea88092831224a04654f1a2780000. Attempt 23507
I iterate over these vectors in the inner loop waiting for the lucky kernel vector that will zero out not just the first 16 but the first 32 bits of the error polynomial. After 1 hour and 30 minutes of waiting on my MacBook Pro, I get the reward:
Error polynomial: c3579192582b50d19bbb377900000000. Attempt 23529
Trying an existential forgery: plainplainplainp�NH��mP^�8��.� �ainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplai
The garbled second block of ciphertext is quite visible in the above output. And I got this outcome with a bit less than the expected amount of tries — 65536.
The relevant code is here.
Incredible, by getting hold of one 2MiB-long ciphertext we are able to forge a new one that differs from the original in 17 blocks and that passes the authentication check during decryption. This is a total failure at CCA security that GCM is supposed to provide.
Recovering the authentication key
In the previous step I was generating different forged coefficients whose Ad matrix had the first 16 rows as zeros and was waiting that eventually one modification to the coefficients would zero out not just the first 16 bits of the error polynomial, which was guaranteed by virtue of the first 16 rows of Ad being zeros, but 32 bits. When that happened rows 16 through 31 of Ad (zero-based counting) were unlikely all zeros and yet the following equality held:
Ad·h = e, where e is a column vector whose first 32 elements are zeros, it represents the error polynomial.
Of these 32 zeroes in e the first 16 were zeros because the first 16 rows of Ad were zeroes. However the next 16
were zeroes because of a linear relationship between rows 16 through 31 of Ad and 16 bits of the authentication key h.
Quoting Niels:
We already knew the first 16 bits were zero, but the fact that the other 16 bits are zero gives us 16 linear equations on the bits of H.
If we copy these non-zero rows 16 through 31 of Ad into a new matrix called K, we have the following equation:
K · h = 0 (1)
[16x128] [128x1] [16x1]
Solving this equation for h delivers up 16 bits of h. The crux of this last part of the attack is in finding more forged coefficients that zero out the first 32 bits of the error polynomial while their zero-out only the first 16 rows of the Ad matrix. Every time we come by such a lucky group of forged coefficients, we add rows 16 through 31 of their Ad matrix to K, whereby increasing our knowledge about h by up-to another 16 bits.
Interestingly, there turns out to be a faster way of recovering the next 16 bits of knowledge about the authentication key.
Looking at equation (1), we notice that h is an element of the kernel (aka the nullspace) of K. If we put the vectors
of the kernel into a new matrix X, we’ll get a 128x112 matrix. Why 112 columns? Because K contains only 16 elements
of the 128-dimensional vector space. Now we take advantage of the fact that X contains knowledge about 16 bits of
the authentication key:
X · h' = h (2)
[128x112] [112x1] [128x1]
Thus, with X known, we only need to find h’, which is a smaller task than finding h. For properly forged coefficients Ad·h = 0. We can now rewrite it as:
Ad · X · h' = 0 (3)
[128x128] [128x112] [112x1] [128x1]
Instead of searching for forged coefficients that zero-out the first 16 rows of Ad, we will search for forged coefficients that zero-out the first rows of Ad·X. Ad·X has dimension 128x112, which is smaller than that of Ad. We use our good old dependency matrix T of dimensions m x 17·128 to accomplish that. However to zero out the first 16 rows of Ad·X, we will fill in its columns with elements of Ad·X. To tackle this I slightly modified my produceDependencyMatrixTransposed method. Quoting Niels on zeroing out rows in Ad·X:
Forcing a complete row to zero only requires 112 free variables, so for the next forgery attempt we can use our 17 × 128 free variables in the Di values to zero 19 rows of the matrix AD · X. This improves the forgery probability to 2-13.
Actually the size of the first dimension m of T [m x 17·128] should be adjusted per iteration to be min(tLen-1, 17·128 / ncols(X)) · ncols(X). As @spdevlin puts it:
The general picture is that if we have n·128 bits to play with, we can zero out (n·128) / (ncols(X)) rows. Just remember to leave at least one nonzero row in each attempt; otherwise you won’t learn anything new.
And on we go, every new success at an existential forgery (i.e. with zeroing out the first 32 bits of the error polynomial) reveal new bits of the authentication key. I slightly modified the code that carries out the existential forgery attack to calculate K, X, after each successful forgery and to keep on running until the rank of K reaches 127.
Now I let the code run and watch it happen :-)
Search for the authentication key started
Attempt 2113. Success with existential forgery. Error polynomial: c2b07aea1c2836f7af2443a300000000
First KB of plaintext:
plainplainplainp���H��h�`��Oainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainpl
Size of K: 16, rank of K: 16
Attempt 8363. Success with existential forgery. Error polynomial: b015d58d06190fcdb36017fe00000000
First KB of plaintext:
plainplainplainp*���ۣ,go�/ainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainp
Size of K: 29, rank of K: 29
Attempt 15245. Success with existential forgery. Error polynomial: 7163d8c0a76cfaa8eb3cd68500000000
First KB of plaintext:
plainplainplainp:�ձ�!C>�4��7a�ainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainpl
Size of K: 40, rank of K: 40
Attempt 15562. Success with existential forgery. Error polynomial: eeb47bbeacdb13058eb7aea900000000
First KB of plaintext:
plainplainplainp�:��y@����І���dainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainpl
Size of K: 48, rank of K: 48
Attempt 15605. Success with existential forgery. Error polynomial: 42cf09a3e378809ffe407b800000000
First KB of plaintext:
plainplainplainp���\�;p�q�m)%��ainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainp
Size of K: 53, rank of K: 53
Attempt 15618. Success with existential forgery. Error polynomial: f73d29205bc9977b3c656e5a00000000
First KB of plaintext:
plainplainplainp"-t�'� �7���B�ainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainpl
Size of K: 56, rank of K: 56
Attempt 15624. Success with existential forgery. Error polynomial: 5d87389b8ff38913a36b79df00000000
First KB of plaintext:
plainplainplainp�����:w)p�:�%�
�ainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainpl
Size of K: 56, rank of K: 56
Attempt 15625. Success with existential forgery. Error polynomial: 51b8daa55ef77b233f7bebc300000000
First KB of plaintext:
plainplainplainp�G��p�����
[�Zainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainpla
Size of K: 58, rank of K: 58
Attempt 15626. Success with existential forgery. Error polynomial: d33117e6b579b79eba08715a00000000
First KB of plaintext:
plainplainplainp�&Ծih�[�ainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplain
Size of K: 59, rank of K: 59
Attempt 15629. Success with existential forgery. Error polynomial: 31d749d6222b943bea11115100000000
First KB of plaintext:
plainplainplainpQ�f�Pxm�r���1P�ainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainp
Size of K: 60, rank of K: 60
Attempt 15630. Success with existential forgery. Error polynomial: a313b46c133df8d194de234a00000000
First KB of plaintext:
plainplainplainp����GbBf� �����ainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplai
Size of K: 61, rank of K: 61
Attempt 15631. Success with existential forgery. Error polynomial: 848037e89964799e6e3f766400000000
First KB of plaintext:
plainplainplainpdj<��
����;��rainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainpl
Size of K: 62, rank of K: 62
Attempt 15641. Success with existential forgery. Error polynomial: 7296c12618a0d9d9387d75d300000000
First KB of plaintext:
plainplainplainp��*y�zb��2ނ]7�ainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainpl
Size of K: 63, rank of K: 63
Attempt 15643. Success with existential forgery. Error polynomial: 88597d4eea708f0f8a0e275d00000000
First KB of plaintext:
plainplainplainp�W~�e��_�����E�ainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainp
Size of K: 64, rank of K: 64
Attempt 15644. Success with existential forgery. Error polynomial: 5372438167bf6364e07cfbce00000000
First KB of plaintext:
plainplainplainp����4���-c
mainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainp
Size of K: 65, rank of K: 65
...
...
Attempt 15774. Success with existential forgery. Error polynomial: bcbc44bd96fb859a90e9d59b00000000
First KB of plaintext:
plainplainplainp���~^Ő�#sϕ�,eainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainpl
Size of K: 125, rank of K: 125
Attempt 15780. Success with existential forgery. Error polynomial: 26873dae13c32c938f90085200000000
First KB of plaintext:
plainplainplainp�O�e9ωbd�
�x��ainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainp
Size of K: 126, rank of K: 126
Attempt 15785. Success with existential forgery. Error polynomial: 135dc814a51c1baef23bd4c600000000
First KB of plaintext:
plainplainplainp'!o�?D�n)�M��$ainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplain
Size of K: 127, rank of K: 127
Recovered authentication key: 2e1e3d193f3ab806eb6b79a6f75e6ef6
Actual authentication key: 2e1e3d193f3ab806eb6b79a6f75e6ef6
Thus after 15785 calls to the decryption oracle, I am able to fully recover the authentication key. Note that as we recover more and more bits of the authentication key, the number of oracle quiries required to obtain further bits decreases exponentially.
The main test of this challenge finally passes!
@DisplayName("https://toadstyle.org/cryptopals/64.txt") @Test
void challenge64() throws NoSuchAlgorithmException, NoSuchPaddingException, InvalidKeyException, BadPaddingException, IllegalBlockSizeException {
int tLen = 32; /* The minimum allowed authentication tag length for GCM */
KeyGenerator aesKeyGen = KeyGenerator.getInstance("AES");
SecretKey key = aesKeyGen.generateKey();
// Going for 2^21 bytes of plain text => 2^17 blocks
// How long should be the plain text to mount an existential forgery on GHASH? Ideally it should be
// 2^(tLen+1) blocks long. This will however be too much: 64 GB. So we will need to go for
// 2^17 blocks, which is 2 MiB, and then expect to zero out another 16 bits by trial and error.
byte[] nonce = new byte[12], plainText = Set8.getPlainText("plain", (tLen >> 1) + 5), pTxt2,
cTxt1, cTxt2, assocData = {};
new SecureRandom().nextBytes(nonce);
GCM gcm = new GCM(key, tLen);
// Oracle that will be used to verify if forged messages authenticate
UnaryOperator<byte[]> gcmFixedKeyAndNonceDecipherOracle = x -> {
try {
return gcm.decipher(x, assocData, nonce);
} catch (BadPaddingException | IllegalBlockSizeException e) {
return null;
}
};
// Oracle that will be used to calculate the error polynomial, not needed for the attack per see
// but makes it run faster as calculating the error polynomial is faster than deciphering the entire ciphertext
BiFunction<PolynomialGaloisFieldOverGF2.FieldElement[], PolynomialGaloisFieldOverGF2.FieldElement[], PolynomialGaloisFieldOverGF2.FieldElement>
gcmFixedKeyAndNonceErrorPolynomialOracle = gcm::ghashPower2BlocksDifferences;
GCMExistentialForgeryHelper h = new GCMExistentialForgeryHelper(cTxt1, plainText.length, tLen,
gcmFixedKeyAndNonceDecipherOracle, gcmFixedKeyAndNonceErrorPolynomialOracle);
// Attempt at an existential forgery and authentication key recovery
h.recoverAuthenticationKey();
pTxt2 = gcm.decipher(h.getForgedCiphertext(), assocData, nonce);
// Confirm that the existential forgery succeeds and that we don't get the bottom (represented as null)
assertNotNull(pTxt2);
// Confirm that the forged ciphertext decrypts into something else than the original plaintext
assertFalse(Arrays.equals(plainText, pTxt2));
System.out.printf("Recovered authentication key: %s%nActual authentication key: %s%n",
h.getRecoveredAuthenticationKey(), gcm.getAuthenticationKey());
// Confirm that the recovered authentication key matches the actual one
assertEquals(gcm.getAuthenticationKey(), h.getRecoveredAuthenticationKey(),
"Authentication key not recovered correctly");
}
The total time of the full attack on my MacBook Pro amounted to 3 hours and 5 minutes. Can it be sped up?
Actually yes. The code that tries different random values for forged coefficients in my
GCMExistentialForgeryHelper.recoverAuthenticationKey method can be parallelized to take advantage of the multiple
cores, which will let the attack succeed in about a quarter of an hour.
Conclusions
How bad is this attack when it comes to real crypto systems at large? Well, TLS (the most active user of GCM) uses the maximum length of the authentication tag in those modes that use GCM such as TLS_ECDHE_RSA_WITH_AES_128_GCM_SHA256. Moreover TLS restricts the length of its records to 16 KB. Using this attack it will only let assuredly forge 9 bits per TLS record. Trial and error to recover more bits will not work as TLS will terminate the session after receiving the first wrongly forged ciphertext.
Can this attack be hypothetically extended over multiple TLS packets? That is, can one forge a new set of short ciphertexts up to 210 blocks long, i.e. seeing many such records when the total size of data transmitted over a TLS session is large?
t1 = s1 + c1_1*h + c1_2*h^2 + c1_3*h^3 + ... + c1_10*h^10
t2 = s2 + c2_1*h + c2_2*h^2 + c2_3*h^3 + ... + c2_10*h^10
....
tm = sm + cm_1*h + cm_2*h^2 + cm_3*h^3 + ... + cm_10*h^10
Fortunately also no. Even though individual records of one session share the same authentication key h, they each have their unique authentication tag.
Why is this attack possible in the first place? The reason is two-fold:
-
GHASH is calculated in GF(2128). Multiplication by a constant and squaring are linear operations in that field. GHASH makes use of multiplications by a constant and squaring. Linear relationships in cryptography are recipes for trouble. This is what makes it possible to achieve a collision in the 32 bits of GHASH, which this attack exploits. Avoiding linear relationships is the reason why all block ciphers such as AES or even DES go to such lengths to ensure that their S-boxes exhibit non-linear behavior. Were AES’s S-boxes linear, AES encryption would boil down to multiplying a large [128x2176] matrix over GF(2) by a column vector [2176x1] made up of a block of plaintext and the 16 round keys derived from the encryption key. So that the entire AES would be represented in this [128x2176] matrix, which would make it trivial to recover an encryption key after seeing just a few plaintext-ciphertext pairs. Dan Boneh gives an excellent explanation of this.
-
GHASH is a one-time MAC, meaning that it can only be used once for the same authentication key. To turn it into a many-time MAC, GCM uses the Carter-Wegman MAC construction:
AuthTag((k, h), m) = E(k, r) ^ GHASH(h, m)where:- k is the encryption key that is passed to GCM by the user;
- h is the authentication key, which GCM derives from the encryption key passed by the user
h = E(k, 0) - r is randomness, which GCM derives from the encryption key and the nonce provided by the user
r = E(K, nonce || 1)
The resulting MAC is many-time secure.
This is all nice and backed by security theorems if the full GHASH tag size of 128 bits is used. If the user chooses a short tag size of, say 32 bits, and we manage to make our forged blocks of ciphertext produce the same 32 bits of GHASH as the legit ciphertext, the xor’ing with with a block of the keys stream doesn’t spread the 32 bits of the GHASH that we managed to forge. And when truncating the resulting AuthTag to the 32 bits before appending it to the ciphertext, GCM passes exactly the 32 bits that we succeeded in forging. This could’ve been fixed by adopting a construction similar to that used by CWC
AuthTag((k, h), m) = E(k, r) ^ E(k, GHASH(h, m)). As you can see, here we encrypt the resulting GHASH before xoring it with the block of the keystream. This AES encryption shuffles and diffuses the 32 bits we managed to forge, whereby rendering this attack useless. Unfortunately the designers of GCM didn’t make use of this solution.
In conclusion I can only repeat the advice given by Niels in his paper:
- If you use GCM, only use it with the maximum tag size of 128 bits. SUN made the right choice in the standard SunJCE cryptography provider in the JRE that flat-out refuses to accept tag lengths fewer than 96 bits.
- If for whatever reason you need to use smaller tags, please use another mode of authenticated encryption supported by NIST such as CCM.
Challenge 65. Truncated-MAC GCM Revisited: Improving the Key-Recovery Attack via Ciphertext Length Extension
Challenge 65 continues with making the attack outlined by Niels Ferguson in his Authentication weaknesses in GCM paper more generic. It’s actually quite admirable that @spdevlin created such a fascinating challenge out of a small paragraph at the end of the paper:
There are small improvements that can be made to this attack. The block that corresponds to D0 of the error polynomial encodes the message length. If the length of the message is not a multiple of 16, then the attacker can extend the message length by appending zero bytes to the ciphertext. This changes only the length encoding in D0. By introducing a nonzero D0, the all-zero solution is no longer possible when we solve for suitable Di values. This means that the attacker can zero out k bits of the tag using only k Di’s, rather than the k + 1 we had before. As the efficiency of the attack is dominated by finding the first successful forgery, this doubles the efficiency of the attack.
Well, easier said than done. To solve the challenge in the most elegant way one needs to tackle three problems:
- Making the attack work when the size of ciphertext is not a multiple of blocksize. Going about it in the same way we crafted the previous attack would not be efficient. The last bytes of ciphertext before the authentication tag are not a multiple of blocksize, therefore the coefficient c2 of c2·h2 will never be full 128 bits, which reduces the number of free variables we can play with. This attack manages to squeeze 128 free variable out of c2.
- Figuring out how to zero out not just 16 rows of Ad in the first existential forgery attempt, but 17 rows with the same number of free variables we had in the previous challenge.
- Once the previous two are solved, how to recover further bits of the authentication key faster with partial knowledge
of the key captured in matrix
X. It is a bit more involved than in the previous challenge.
Making the attack work when plaintext is not a multiple of blocksize
When ciphertext is not a multiple of blocksize, GCM pads it with zeros to be a multiple of blocksize before calculating the authentication tag. This affects the coefficient c2 in the polynomial in the indeterminate h over GF(2128): t = s + c1·h + c2·h2 + c3·h3 + … + cn·hn, where c2 is the last block of the ciphertext before the tag, and cn is the first (assuming that the plain text was 2n blocks long).
As a result of the padding a number of bits in c2 will be zeroes. Worse, we will not be allowed to manipulate these zero bits during the attack because doing so implies changing the length of the plaintext/ciphertext and hence requires adjusting c1, which is constructed from a block encoding the length of associated data (the first 8 bytes) and plaintext (the next 8 bytes). c1 was the only coefficient of h2^i terms that we left alone in the previous challenge. So what do we do? We create a new c1, which encodes the padded length of the plaintext. This gives us the 128 free variables from c2 to play with. However there’s a price to pay because the difference d1 = c1 - c’1 between the original and forged blocks encoding the lengths will not be zero any more. As a result we are no longer able to rely on the equation
T · d = 0
to zero out the first rows in Ad. It’s easy to see why. We calculate the dependency matrix T by flipping
bits in the coefficients c2, c4, c8, …, c2^17 — exactly as we did before.
and we solve for d to zero out the first rows in Ad. However this will not work because we also changed c2^0
and hence the summand Ad0 (the matrix representation of the difference between the original c1 and
our forged c’1 encoding the longer plaintext length) became a non-zero matrix (it was a zero matrix in the
previous challenge). So we need to solve a different equation now
T · d = t
where t represents a column vector of differences induced to the cells of Ad by our new non-zero matrix Ad0.
Here’s how this looks in code:
if (Ad0 != null) { /* We need to solve for T * d = t */
boolean[] t = new boolean[m];
// Ad is constructed over c2, c4, c2^17. Ad0 is constructed over c1
boolean[][] T = transpose(tTransposed), Ad = calculateAd(forgedCoeffs);
for (int i = 0; i < m; i++) {
// t is the nonzero difference in the first n rows of AdX induced by our tweak to the length block.
t[i] = Ad[i / ncolsX][i % ncolsX] ^ Ad0[i / ncolsX][i % ncolsX];
}
To solve this equation I equipped my BooleanMatrixOperations.gaussianElimination method
with a new parameter indicating whether to perform Gaussian elimination to reduced low row echelon form or to low echelon form.
I then append column vector
t to the dependency matrix T and bring this augmented matrix to reduced row echelon form:
boolean[][] tWithCol = appendColumn(T, t);
rank = gaussianElimination(tWithCol, tTransposed.length, null, true);
d = extractColumn(tWithCol, tTransposed.length);
Frequently T will not have any linearly dependent rows and the assertion
assert Arrays.equals(multiply(T, d), t);
will hold. However sometimes there’ll be linearly dependent rows. In this case I take my chance on the resulting
system of linear equations to be consistent and extract the bits of d from linearly independent rows:
if (rank < T.length) {
// It is still possible for T, t to be consistent if the dependent row of T have the same values in t
int h = 0, k = 0;
while (h < tWithCol.length && k < tWithCol.length) {
if (tWithCol[h][k]) {
d[k] = tWithCol[h][tTransposed.length];
h++; k++;
} else {
d[k] = false; // The corresponding row of T is linearly dependent on an earlier row
k++;
}
}
}
So now we have one d vector of flips to try. How do we get more? We turn to the following linear algebra theorem.
I.e. we calculate the kernel of T, as we did in the previous challenge, and add our newly found d to each vector in
the kernel. This is our new set of bit flips to try to arrive at an existential forgery.
We are not done though. The code that calls the Oracle should also be modified as should be the code that extracts
and replaces 2i-th blocks of ciphertext (counting from the end). This is a simple generalization of the
extractPowerOf2Blocks and replacePowerOf2Blocks methods I created for the previous challenge. extractPowerOf2Blocks
needs to cater to cases when plaintext is not a multiple of blocksize, while GCM.replacePowerOf2Blocks should do the same
and also get the capability to expand the last block of ciphertext to be a multiple of blocksize.
Figuring out how to zero not just 16 rows of Ad but 17
Now that we solve T · d = t rather than T · d = 0 (where t is not a zero vector), a zero-vector solution d is
not possible. So what we do is construct a larger T than in the previous challenge. Its dimension used to be [128·17x128·16],
now we increase the second dimension to be as big as the first so the dimension of T becomes [128·17x128·17]. This
indeed allows us to zero out 17 rows of Ad. However there’s a wrinkle. If we calculate the kernel
of this large T matrix, it will frequently be empty or have one or two vectors max. In fact it will have as many
vectors as there are linearly dependent rows in this large T. Often there will be none.
To tackle this I do the following: I solve for T · d = t using the large T matrix [128·17x128·17] and get one vector
that assuredly zero’s out the first 17 rows of Ad. Then I reduce the second dimension of T to [128·17x128·16]
and find the kernel of this smaller T. This gives me a kernel with the expected number of 128 vectors. I then add d to each
one of them and end up with: 1) one vector d which assuredly zeros out the first 17 rows of Ad, 2)
128 kernel[i] + d vectors that zero out 16 rows of Ad and, maybe, 17. Here’s how it looks in code:
if (mReduced < m) {
tTransposed = copy(tTransposed, mReduced);
}
boolean[][] preKernel = kernelOfTransposed(tTransposed);
kernel = new boolean[preKernel.length + 1][];
kernel[0] = d;
for (int i=0; i < preKernel.length; i++) {
kernel[i + 1] = add(preKernel[i], d);
}
Recover further bits of the authentication key faster with partial knowledge of the key captured in matrix X
This actually turned out to be the most strenuous part of the attack. As @spdevlin put it:
The dimensions of T and d will change. You should be able to work out how with a bit of deliberation.
A bit of deliberation for sure :-) The two tricky bits for me were:
- To ensure I find all 128 bits of
tin the
Ad · X · h' = t
[128x128] [128x112] [112x1] [128x1]
equation. This requires that the dimensions of the dependency matrix T I use to solve T · d = t are always
[128·17x128·17] while in the previous challenge it was not necessary
- Not zeroing out too many bits of the error polynomial. As the number of column vectors in X shrinks, we may end up zeroing out many more than 16 bits of the error polynomial. We thus need to have enough elements in X to solve Ad·X·h = t. This requires that the second dimension of X be as large as the number of power 2 blocks we have to play around with (17 in out case). However that will likely lead to us zeroing out many more bits of the error polynomial than tLen. Since the Oracle only tells us whether we correctly zeroed out tLen ones (32), we cannot assuredly rely on the other bit being zeroed out, even though it is likely to be the case. To combat that I refrain from shrinking the second dimension of X that is used in constructing the dependency matrix further than thrice the number of coefficients we can play with (not counting c1).
In code this can all be found in the GCMExistentialForgeryHelper::replaceBasis and GCMExistentialForgeryHelper::recoverAuthenticationKey methods.
And here comes the final go at a forgery and an eventual recovery of the authentication key (with an authentication tag of 16 bits to save computing time)
Search for the authentication key started
Attempt 12. Success with existential forgery. Error polynomial: bb0ad5a9c719ef02c59ea28ae8ec0000
First KB of plaintext:
plainplainplainp���;e��Tq>`ݰ��ainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainp
Size of K: 8, rank of K: 8
Kernel size: 73
...
...
...
Attempt 670. Success with existential forgery. Error polynomial: 8b10b67c7cbd39b4ca6e76e69a3b0000
First KB of plaintext:
plainplainplainp���
23x��\zf�-��ainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplai
Size of K: 116, rank of K: 116
Kernel size: 817
Attempt 679. Success with existential forgery. Error polynomial: cfda75f9c1cdb62221c7164f3f770000
First KB of plaintext:
plainplainplainp��!�� &7z%���ainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainpl
Size of K: 120, rank of K: 120
Kernel size: 817
Attempt 702. Success with existential forgery. Error polynomial: 374a436456f6ff0347793e51e1740000
First KB of plaintext:
plainplainplainp�-.��'}����<ainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplai
Size of K: 124, rank of K: 124
Kernel size: 817
Attempt 771. Success with existential forgery. Error polynomial: 816fbe039b8ad09cae74819230a80000
First KB of plaintext:
plainplainplainp+ ��l&��(����uI(ainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainplainpla
Recovered authentication key: ee3349e46e4d8a32790c11dd49b906b9
Actual authentication key: ee3349e46e4d8a32790c11dd49b906b9
Challenge 66. Exploiting Implementation Errors in Diffie-Hellman
Challenge 66 picks up where Challenge 59 left off and shows an exploit based on a faulty implementation of arbitrary-precision integers. Of all the challenges in Set 8 this is by far the least strenuous. It took me the least effort as it builds upon code developed in the earlier challenges. While the problem explanation is pretty self-explanatory, some notes are nevertheless worth making.
Define an oracle that accepts a point Q, multiplies it by d, and returns true or false depending upon whether a fault is triggered. In a realistic setting, this could be an endpoint that computes the ECDH handshake and decrypts a message. You can build this out if you’re feeling fancy, but the artificial oracle is okay too.
I chose the fancy path as it is more realistic and reused the server-side code from Challenges 59 and 60 that represents Bob’s contribution to ECDH. Remarkably the only change I needed to make for Bob is to ensure his private key is always of the maximum possible length (i.e. the same number of bits as in the order of the curve).
private void init(ECGroupElement g, BigInteger q) {
if (ecg == null || !ecg.equals(g.group()) || !this.g.equals(g)) {
ecg = g.group();
this.g = g;
DiffieHellmanHelper dhh = new DiffieHellmanHelper(ecg.getModulus(), q);
BigInteger pk;
do { /* Ensure the private key has the maximum possible number of bits */
pk = dhh.generateExp().mod(q);
} while (pk.bitLength() != q.bitLength());
privateKey = pk;
}
}
Rather than mess up with the Elliptic curve classes WeierstrassECGroup and MontgomeryECGroup, which I implemented without flaws for earlier problems, I created a new one called FaultyWeierstrassECGroup. It differs from its legit counterpart in the implementation of the scale and combine methods. Excepting this, it works the same as WeierstrassECGroup:
@Test
void faultyCurveForChallenge66() {
// Using Bitcoin's secp256k1
FaultyWeierstrassECGroup secp256k1 = new FaultyWeierstrassECGroup(CURVE_SECP256K1_PRIME, ZERO, valueOf(7), CURVE_SECP256K1_ORDER, valueOf(1000));
BigInteger baseX = new BigInteger("79BE667EF9DCBBAC55A06295CE870B07029BFCDB2DCE28D959F2815B16F81798", 16);
FaultyWeierstrassECGroup.ECGroupElement secp256k1Base = secp256k1.createPoint(baseX, secp256k1.mapToY(baseX));
BigInteger q = secp256k1.getCyclicOrder();
WeierstrassECGroup secp256 = new WeierstrassECGroup(CURVE_SECP256K1_PRIME, ZERO, valueOf(7), CURVE_SECP256K1_ORDER, valueOf(1000));
WeierstrassECGroup.ECGroupElement secp256Base = secp256.createPoint(baseX, secp256k1.mapToY(baseX));
// Verify that the faulty curve behaves correctly
assertEquals(secp256k1Base.scale(valueOf(58)).getX(), secp256Base.scale(valueOf(58)).getX());
assertEquals(secp256k1Base.scale(valueOf(58)).getY(), secp256Base.scale(valueOf(58)).getY());
assertEquals(secp256k1Base.scale(valueOf(62)).getX(), secp256Base.scale(valueOf(62)).getX());
assertEquals(secp256k1Base.scale(valueOf(62)).getY(), secp256Base.scale(valueOf(62)).getY());
}
The core of the attack lies in the scaleForChallenge66, findPointWithFaultAtBitIndex, and breakChallenge66 methods. The main point to understand is the following piece in the problem description:
… If it triggers the fault, k[2] = 0 (probably.) Probably? Well, sure. There is, of course, a chance for false positives. Since we’re treating faults as random, there is a small but nonzero chance your input point will trigger a fault on some later step.
If you get it, the rest of the challenge is a piece of cake to finish.
I experimented with different values for the incidence rate of faults and eventually settled for incidence = 100000.
Initially I wanted to make use of both 1) outcomes that don’t trigger a fault (which is guaranteed to be free of false positives),
and 2) those that do. As proposed by @spdevlin:
Even in the presence of uncertainty, positive results have value. You can calculate the probability of a false positive and determine whether you have enough confidence to proceed.
With some assumptions this probability is not that difficult to calculate. The probability of a fault in each invocation of
scale is approximately 1/incidence. Therefore the probability of no fault in an invocation is 1 - 1/incidence.
The maximum possible number of invocations of scale after processing private key bit with index idx is numSteps = 2 * idx.
So the upper bound on the probability of no faults in these following steps is (1-1/incidence)numSteps.
My code looked like this:
double probability = 1 - 1 / incidence.doubleValue();
while (idx > 0) {
FaultyWeierstrassECGroup.ECGroupElement point = findPointWithFaultAtBitIndex(group, pk, idx, isLeftBranch);
try {
bob.initiate(base, order, point);
} catch (IllegalStateException ex) {
// Even in the presence of uncertainty, positive results have value.
//
// The maximum possible number of tries after this idx is numSteps = 2 * idx.
// The low bound on the probability of no faults in these following steps is (1-1/incidence)^numSteps
if (Math.pow(probability, idx << 1) > .9999) {
if (!isLeftBranch[0]) {
pk = pk.setBit(idx);
}
} else continue;
}
However I soon abandoned the idea as for it to work Bob is expected not to do any further operations that might trigger a fault after he calculates the shared secret from Alice’s point A (her public key). This will not hold in a real-world setting as Bob will then go ahead to calculate his public key and this step might also trigger a fault. It is possible to make the code representing Bob cooperate with an attacker by propagating faults occurring when calculating the shared secret while swallowing those happening when computing Bob’s public key. However such an approach would be utterly unrealistic.
/**
* @param g a generator of a (sub)group of the elliptic curve group that g is a member of
* @param q the order of the generator
* @param A Alice's public key
*/
public Set8.Challenge59ECDHBobResponse initiate(ECGroupElement g, BigInteger q, ECGroupElement A) throws RemoteException {
init(g, q);
macKey = Set8.generateSymmetricKey(A, privateKey, 32, Set8.MAC_ALGORITHM_NAME); // <-- We expect a fault here
mac.init(macKey);
return new Set8.Challenge59ECDHBobResponse(
g.scale(privateKey), Set8.CHALLENGE56_MSG, mac.doFinal(Set8.CHALLENGE56_MSG.getBytes()) ); // <-- But this can also trigger a fault
Even without this optimization, the time to fully recover they key on a single thread for the curve from Challenge 59 was a meager 4 minutes:
@DisplayName("https://toadstyle.org/cryptopals/66.txt")
@ParameterizedTest @ValueSource(strings = { "rmi://localhost/ECDiffieHellmanBobService" })
// The corresponding SpringBoot server application must be running.
void challenge66(String url) throws RemoteException, NotBoundException, MalformedURLException {
BigInteger incidence = valueOf(100_000);
FaultyWeierstrassECGroup group = new FaultyWeierstrassECGroup(new BigInteger("233970423115425145524320034830162017933"),
valueOf(-95051), valueOf(11279326), new BigInteger("233970423115425145498902418297807005944"), incidence);
FaultyWeierstrassECGroup.ECGroupElement base = group.createPoint(
valueOf(182), new BigInteger("85518893674295321206118380980485522083"));
BigInteger q = new BigInteger("29246302889428143187362802287225875743");
BigInteger b = Set8.breakChallenge66(base, q, url, incidence);
ECDiffieHellman bob = (ECDiffieHellman) Naming.lookup(url);
assertTrue(bob.isValidPrivateKey(b));
}
Point found after 220 tries
Point found after 541 tries
Point found after 114 tries
Recovered bit index # 123
pk: 10000000000000000000000000000000
...
...
Recovered bit index # 4
pk: 115f0d01b0f5b1f821a9740366c59020
Point found after 197 tries
Recovered bit index # 3
pk: 115f0d01b0f5b1f821a9740366c59028
Point found after 713 tries
Recovered bit index # 2
pk: 115f0d01b0f5b1f821a9740366c59028
Point found after 664 tries
Recovered bit index # 1
pk: 115f0d01b0f5b1f821a9740366c5902a
Point found after 756 tries
Recovered bit index # 0
pk: 115f0d01b0f5b1f821a9740366c5902a
As a final note, the challenge does make two assumptions apart from a faulty implementation of arbitrary-precision integers on Bob’s side, namely that:
- Bob will naively hang on to the same private key across all new sessions with Alice.
- Bob will ensure his private key is always of the same bit length and that this length is known to Alice.